条件付き最大最小値に関する問題を扱っていきます。
(例題1)
1つの頂点から出る3辺の長さが \(x,y,z\) である直方体を考える、この直方体の辺の長さの総和が\(24\),表面積が\(18\)であるとする。
(1)\(x\)のとりうる範囲を求めよう。条件より
\(y+z=6-□x\)
\(yz=□x^2-□x+9\)
よって、\(y,z\)はある2次方程式の2つの正の実数解と考えられる。このことから、求める\(x\)の範囲は、\(□<x≦□\) (ただし、\(x=□\)を除く) である。
(2)この直方体の体積\(V\)の最大値を求めよう。
\(V=xyz=□x^3-□x^2+9x\)
だから、\(V\)の最大値は\(□\)である。このときの3辺の長さを\(x_0,y_0,z_0\) (\(x_0≦y_0≦z_0\)) とすると、\((x_0,y_0,z_0)=(□,□,□)\) である。
(解答)
(1)
\(x,y,z\)は3辺の長さなので正の数ですが、例えば\(x\)が\(100\)とかいう大きい数だと、長さの総和が\(24\)より、\(y\)か\(z\)が負の数になってしまうので、\(x\)がある範囲にあるという制限が必要になってきます。それを聞いているのが(1)ですが、\(y,z\)の和と積が\(x\)で表されるので、2次方程式が正の解をもつという条件に帰着できて、そこから\(x\)の範囲が分かりますが、これだけだと\(y,z\)が正の数になるということしか保証されていないので、\(x>0\) も、もちろん加えます。
(1)
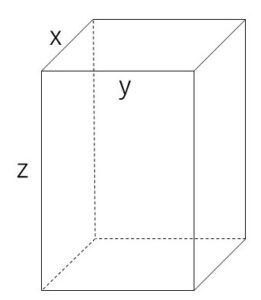
辺の長さの総和が\(24\),表面積が\(18\)だから、
\(4(x+y+z)=24\)
\(2(xy+yz+zx)=18\)
よって
\(x+y+z=6\)・・・①
\(x(y+z)+yz=9\)・・・②
①より \(y+z=6-x\)
②に代入して整理すると
\(yz=x^2-6x+9\)
\(y,z\) は2次方程式
\(t^2-(6-x)t+(x^2-6x+9)=0\)
の2つの正の実数解なので
(i) \(D≧0\)
(ii) \(y+z>0\)
(iii) \(yz>0\)
(ii),(iii)については、軸と端点で考えてもよいです。(同じ式がでてきます)
(i)より
\((6-x)^2-4(x^2-6x+9)≧0\)
整理して
\(x(x-4)≦0\)
\(0≦x≦4\)
(ii)より
\(6-x>0\)
\(x<6\)
(iii)より
\(x^2-6x+9>0\)
\((x-3)^2>0\)
\(x≠3\)
したがって \(x>0\) も加えると
\(0<x≦4\) (\(x=3\)を除く)
(2)
(1)より
\(V=xyz=x(x^2-6x+9)\)
\(=x^3-6x^2+9x\)
\(V’=3(x-1)(x-3)\)
増減表は
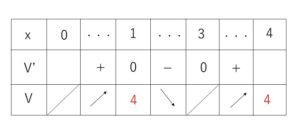
よって、最大値は \(4\)
このとき、\(x_0=1,4\)
\(x_0=1\) のとき(1)より
\(y+z=5\)
\(yz=4\)
だから、2次方程式
\(t^2-5t+4=0\) の解を考えて
\((t-1)(t-4)=0\) , \(y_0≦z_0\) より
\(y_0=1\), \(z_0=4\) (\(x_0≦y_0\)を満たす)
したがって
\((x_0,y_0,z_0)=(1,1,4)\)
\(x_0=4\) のとき
\(y+z=2\) より、\(y<2\) だから不適。
(例題2)
\(x,y,z\) は \(y+z=1\), \(x^2+y^2+z^2=1\) を満たす実数とする。
(1)\(x\)のとりうる値の範囲を求めよ。
(2)\(x^3+y^3+z^3\) を\(x\)の関数として表し、その最大値と最小値を求めよ。
文字3つについて2つ条件式があるので実質1変数の最大最小値を求める問題で、しかも文字消去ができる場合です。(例題1)と同様に、\(x\)の取りうる範囲を2次方程式が実数解をもつ条件におとしますが、①\(y,z\)の和と積を考える ②\(y+z=1\) より1文字消去する方法の 2パターンでやりたいと思います。今回は特に正の数などの条件はないので単に実数になることだけを考えます。
(解答)
(1)
\(x^2+y^2+z^2=1\) より
\(x^2+(y+z)^2-2yz=1\)・・・①
①に
\(y+z=1\)
を代入して
\(yz=\displaystyle\frac{1}{2}x^2\)
よって \(y,z\)は2次方程式
\(t^2-t+\displaystyle\frac{1}{2}x^2=0\)
の実数解だから
\(D≧0\) より
\(1-2x^2≧0\)
\(-\displaystyle\frac{1}{\sqrt{2}}≦x≦\displaystyle\frac{1}{\sqrt{2}}\)
※文字消去の方法だと
\(z=1-y\)・・・②
を \(x^2+y^2+z^2=1\) に代入して
\(x^2+y^2+(1-y)^2=1\)
\(y\)について整理すると
\(2y^2-2y+x^2=0\)・・・③
この\(y\)の2次方程式③が実数解をもてばよいので(このとき②より\(z\)も実数となる)
\(\displaystyle\frac{D}{4}≧0\) より
\(1-2x^2≧0\)
\(-\displaystyle\frac{1}{\sqrt{2}}≦x≦\displaystyle\frac{1}{\sqrt{2}}\)
(2)
(1)より
\(y+z=1\)
\(yz=\displaystyle\frac{1}{2}x^2\)
だから
\(x^3+y^3+z^3\)
\(=x^3+(y+z)^3-3yz(y+z)\)
\(=x^3-\displaystyle\frac{3}{2}x^2+1\)
(\(=f(x)\) とおく)
\(f'(x)=3x(x-1)\)
\(-\displaystyle\frac{1}{\sqrt{2}}≦x≦\displaystyle\frac{1}{\sqrt{2}}\) の範囲で増減表は
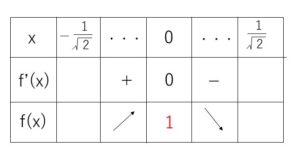
\(f(-\displaystyle\frac{1}{\sqrt{2}})<f(\displaystyle\frac{1}{\sqrt{2}})\) だから
最小値は\(f(-\displaystyle\frac{1}{\sqrt{2}})=-\displaystyle\frac{\sqrt{2}}{4}+\displaystyle\frac{1}{4}\)
最大値 \(1\) (\(x=0\))
最小値 \(\displaystyle\frac{1-\sqrt{2}}{4}\) (\(x=-\displaystyle\frac{1}{\sqrt{2}}\))
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→条件付き最大・最小値②(円の媒介変数) back→他の関数を含む最大・最小値