接線の本数に関する問題について扱っていきます。
(例題1)
\(xy\)平面上に 曲線 \(y=2x^3-6x^2+12x-9\) がある。この曲線の接線で、点\((2,a)\) を通るものが2本あるような\(a\)の値を求めよ。
(解答)
\(y=2x^3-6x^2+12x-9\) 上の点
\((t,2t^3-6t^2+12t-9)\) における接線を考える。
\(y’=6x^2-12x+12\) より、接線の方程式は
\(y=(6t^2-12t+12)(x-t)+2t^3-6t^2+12t-9\)
整理して
\(y=(6t^2-12t+12)x-4t^3+6t^2-9\)
\((2,a)\) を接線が通るので
\(a=(6t^2-12t+12)\cdot2-4t^3+6t^2-9\)
整理して
\(a=-4t^3+18t^2-24t+15\)・・・①
3次関数では接点が異なれば接線も異なるので・・・(注)、①の解の個数(接点の個数)が、接線の本数になります。したがって接線が2本存在するには①が異なる2つの実数解をもてばよいことになります。①はちょうど定数が分離されているので、\(y=\)(右辺) の関数を考えて、\(y=a\)を動かしていきます。
(注)については →(2-5)二重接線 を参照してください。
\(t\)の方程式①が、異なる2つの実数解をもつとき接線が2本存在する。
\(y=-4t^3+18t^2-24t+15\)・・・② とおくと
\(y’=-12(t-1)(t-2)\)
増減表とグラフは次の通り。
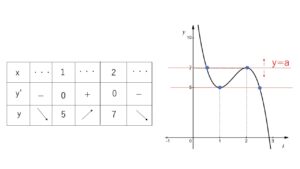
方程式①が異なる2つの実数解をもつような\(a\)の値は、曲線②と \(y=a\) が共有点を2つもつときだから
\(a=5,7\)
(例題2)
\(xy\) 平面上の放物線 \(y=x^2\) を \(C\)で表すとき、平面上の点 \((a,5)\) を通る\(C\)の法線が3本存在するときの\(a\)の値の範囲を求めよ。
(解答)
\(C:y=x^2\) 上の点 \((t,t^2)\) における法線は
\(y’=2x\) より
\(y=-\displaystyle\frac{1}{2t}(x-t)+t^2\) (\(t≠0\))
\(t\)倍して整理すると
\(ty=-\displaystyle\frac{1}{2}x+t^3+\displaystyle\frac{t}{2}\)・・・①
(①で\(t=0\)とすると \(x=0\) になり、これは \((0,0)\)における法線になるので、\(t=0\)でも適する)
①は \((a,5)\) を通るから
\(5t=-\displaystyle\frac{a}{2}+t^3+\displaystyle\frac{t}{2}\)
よって
\(a=2t^3-9t\)・・・②
\(y’=2x\) より、接線の傾きが接点によって異なるので、法線の傾きも接点によって異なるから、異なる点における法線はすべて異なることなります。
したがって\(t\)の方程式②の実数解の個数(点の個数)がそのまま法線の個数になります。
一般に2次関数では、曲線上の点が異なれば法線が異なることなりますが、3次関数の場合には導関数が2次関数(対称な曲線)になるので、異なる点でも接線の傾きが等しくなるところがあるので、法線の傾きが等しくなるところもあり、場合によっては異なる点でも法線が一致することがあります。(それを複法線とよびます)
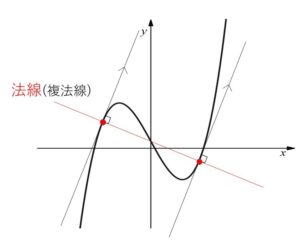
曲線\(C\)は2次関数だから、\(C\)上の異なる点では法線も異なるので
方程式②が異なる3つの実数解をもつとき、法線が3本存在することになる。
\(y=2t^3-9t\)・・・③
\(y=a\)・・・④
③について
\(y’=6(t^2-\displaystyle\frac{3}{2})\) よりグラフは次の通り。
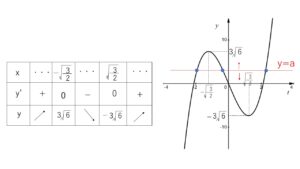
③のグラフと直線④の共有点が3つあるときを考えればよいので
\(-3\sqrt{6}<a<3\sqrt{6}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→接線の本数② back→実数解の個数②