陰関数・媒介変数表示された曲線の接線を、微分を利用して求める例題です。
(例題1)
(1)曲線 \(2x^2-2xy+y^2=5\) 上の 点(\(1,3\)) における接線の方程式を求めよ。
(2)円周 \(x^2+y^2=a^2\) (\(a>0\)) 上の 点\(P(x_0,y_0)\) における接線の方程式を微分を利用して求めよ。
いずれも\(y\)は\(x\)に依存する(\(x\)の関数である)ことを意識して、\(x\)で微分する際に定数扱いしないようにします。
(1)
\(2x^2-2xy+y^2=5\)
において、両辺\(x\)で微分すると(\(xy\)は積の微分、\(y^2\)は合成関数の微分)
\(4x-2\cdot1\cdot y-2x\cdot y’+2yy’=0\)
よって
\(2(y-x)y’=-4x+2y\)
点(\(1,3\)) における接線の傾きは、\(x=1\)、\(y=3\) を代入して
\(y’=\displaystyle\frac{-4+6}{2\cdot2}\)\(=\displaystyle\frac{1}{2}\)
したがって接線の方程式は
\(y-3=\displaystyle\frac{1}{2}(x-1)\)
\(y=\displaystyle\frac{1}{2}x+\displaystyle\frac{5}{2}\)
(2)
\(x^2+y^2=a^2\) (\(a>0\))
両辺\(x\)で微分すると
\(2x+2yy’=0\)
よって
\(yy’=-x\)
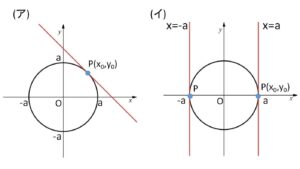
(ア)\(y≠0\) (\(y_0≠0\)) のとき
\(y’=-\displaystyle\frac{x}{y}\) だから
点\(P(x_0,y_0)\) における接線の傾きは
\(y’=-\displaystyle\frac{x_0}{y_0}\) だから、\(P\)における接線の方程式は
\(y-y_0=-\displaystyle\frac{x_0}{y_0}(x-x_0)\)
整理すると
\(x_0x+y_0y=x_0^2+y_0^2\)
\(x_0x+y_0y=a^2\)・・・①
(\(P\)は円周上の点だから、 \(x_0^2+y_0^2=a^2\) )
(イ)\(y=0\) (\(y_0=0\)) のとき
接点は、\(P(a,0)\) または \(P(-a,0)\)
このとき接線はそれぞれ \(x=a\)、\(x=-a\) となるが
①で、\((x_0,y_0)=(a,0)\)、\((x_0,y_0)=(-a,0)\)
としてそれぞれ得ることができる。
以上より接線の方程式は(1つにまとめることができて)
\(x_0x+y_0y=a^2\)
(例題2)
曲線
\(x=t\cos t\)、\(y=t\sin t\)
の \(t=\displaystyle\frac{π}{2}\) に対応する点における接線の方程式を求めよ。
対応する点については\(x,y\)それぞれに、\(t=\displaystyle\frac{π}{2}\) を代入するだけで求めることができます。
(解答)
\(x=t\cos t\)・・・①
\(y=t\sin t\)・・・②
①②をそれぞれ\(t\)で微分して
\(\displaystyle\frac{dx}{dt}=\cos t+t(-\sin t)\)
\(\displaystyle\frac{dy}{dt}=\sin t+t\cos t\)
よって
\(\displaystyle\frac{dy}{dx}=\displaystyle\frac{\sin t+t\cos t}{\cos t-t\sin t}\)
となるから、\(t=\displaystyle\frac{π}{2}\) に対応する点における接線の傾きは、
\(\displaystyle\frac{dy}{dx}=\displaystyle\frac{1+0}{0-\displaystyle\frac{π}{2}}=\)\(-\displaystyle\frac{2}{π}\)
また、\(t=\displaystyle\frac{π}{2}\) に対応する点の座標は①②より
\(x=0\)、\(y=\displaystyle\frac{π}{2}\)
したがって接線の方程式は
\(y-\displaystyle\frac{π}{2}=-\displaystyle\frac{2}{π}(x-0)\)
整理して
\(y=-\displaystyle\frac{2}{π}x+\displaystyle\frac{π}{2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→ある点を通る接線 back→接線・法線の方程式