上に凸(下に凸)の関数と、線分の内分点の関係について見ていきます。
・凸関数と不等式
上に凸(下に凸)の関数のグラフと、そのグラフ上の2点を結ぶ線分の位置関係を、内分点に着目すると次のように表現することができます。
2回微分可能な関数\(f(x)\)について、\(t\)を \(0<t<1\) を満たす実数とすると、
(1)\(f”(x)>0\) (下に凸) のとき
\(tf(x_1)+(1-t)f(x_2)≧f\{tx_1+(1-t)x_2\}\)
(2)\(f”(x)<0\) (上に凸) のとき
\(tf(x_1)+(1-t)f(x_2)≦f\{tx_1+(1-t)x_2\}\)
(解説)
(1)について ((2)も同様なので省略)
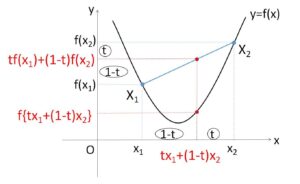
\(x_1≠x_2\) のとき
\(x_t=tx_1+(1-t)x_2=\displaystyle\frac{tx_1+(1-t)x_2}{(1-t)+t}\) (内分点)
より、\(0<t<1\) だから、\(x=x_t\) は \(x=x_1,x_2\) の間にある。
下に凸なので、は線分\(X_1X_2\)は上側に位置しているので、
\(tf(x_1)+(1-t)f(x_2)>f\{tx_1+(1-t)x_2\}\)
が成り立つ。(左辺は線分上の内分点の\(y\)座標、右辺は\(y=f(x)\)上の\(y\)座標)
また、\(x_1=x_2\) のときは2点\(X_1,X_2\)が一致することから
\(tf(x_1)+(1-t)f(x_2)=f\{tx_1+(1-t)x_2\}\)・・・①
となり、等号が成立する。(①で\(x_1=x_2\)としても成り立つことが分かる)
これは\(x_1=x_2\)の場合を含めることが理由で、不等式の等号を成立させることで最小値や最大値を求めることに利用するためです。(ただの大小については対称性より設定しても問題ない)
それと、\(f”(x)≧0\) として \(f”(x)=0\) の場合を含めても同じように不等式は成り立ちます。\(f”(x)=0\) のときは \(f(x)\) が 「1次以下の整式(直線)」となるからです。 (等号成立条件は若干変わる)
ここで、\(t=t_1\)、\(1-t=t_2\) とおきかえると
\(t_1+t_2=1\)、\(0<t_1\ (<1)\)、\(0<t_2\ (<1)\) (\(1\)より小さいはあっても無くてもよい)
となるので、上記不等式を次のように言い換えることが可能です。
(1)\(f”(x)>0\) (下に凸) のとき
\(t_1f(x_1)+t_2f(x_2)≧f(t_1x_1+t_2x_2)\)
(2)\(f”(x)<0\) (上に凸) のとき
\(t_1f(x_1)+t_2f(x_2)≦f(t_1x_1+t_2x_2)\)
(等号は \(x_1=x_2\) のとき成立)
さらにこれを拡張すると、次のイェンゼン(イェンセン)の不等式と呼ばれるものになります。
\(n\)は2以上の自然数とする。\(t_1,t_2,\cdots,t_n\) を \(t_1+t_2+\cdots+t_n=1\)、\(t_1,t_2,\cdots,t_n>0\) を満たす実数とするとき
(1)\(f”(x)>0\) (下に凸) のとき
\(t_1f(x_1)+t_2f(x_2)+\cdots+t_nf(x_n)≧f(t_1x_1+t_2x_2+\cdots+t_nx_n)\)
(2)\(f”(x)<0\) (上に凸) のとき
\(t_1f(x_1)+t_2f(x_2)+\cdots+t_nf(x_n)≦f(t_1x_1+t_2x_2+\cdots+t_nx_n)\)
(等号は \(x_1=x_2=\cdots=x_n\) のとき成立)
(証明)
証明は \(n=2\) の場合を出発とした帰納法か、接線と凸関数の位置関係から示すことができます。
いずれも(1)だけについて証明します。((2)も同様に示せる)
なお、\(n=1\) でも不等式は成り立ちますが(常に等号成立)、あまり有用性がないので省きました。
(証明1)帰納法
(i)\(n=2\) のとき
(上記の流れで成り立つことは分かりますが、改めて証明しておきます。2変数なので差をとって1文字固定で微分する方法をとりたいと思います。他にも平均値の定理を使う方法などもあります)
\(t_1f(x_1)+t_2f(x_2)≧f(t_1x_1+t_2x_2)\)・・・(A)
(\(t_1+t_2=1\)、\(t_1,t_2>0\))
を示したい。\(x_2\)を固定して
\(F(x)=t_1f(x)+t_2f(x_2)-f(t_1x+t_2x_2)\)
とおく。
\(F'(x)=t_1f'(x)-t_1f'(t_1x+t_2x_2)\)
\(=t_1(\color{blue}{f'(x)-f'(t_1x+t_2x_2)})\)
(\((x_1=)x=x_2\) のとき線分の端点が重なるので、このとき差\(F(x)\)が\(0\)になることを意識して、\(f()\) の中身の大小を考えます)
ここで、\(f”(x)>0\) より \(f'(x)\) は単調増加。
また
\(x-(t_1x+t_2x_2)=x-(1-t_2)x-t_2x_2=\)\(t_2(x-x_2)\)
となるから、(単調増加より、中身の小さいほうが小さくなる)
\(x<x_2\) のとき \(f'(x)<f'(t_1x+t_2x_2)\)
\(x=x_2\) のとき \(f'(x)=f'(t_1x+t_2x_2)\)
\(x>x_2\) のとき \(f'(x)>f'(t_1x+t_2x_2)\)
\(t_1>0\) だから
\(x<x_2\) のとき \(F'(x)<0\)
\(x=x_2\) のとき \(F'(x)=0\)
\(x>x_2\) のとき \(F'(x)>0\)
となる。ゆえに \(x=x_2\) のとき\(F(x)\)は最小値
\(F(x_2)=t_1f(x_2)+t_2f(x_2)-f(t_1x_2+t_2x_2)\)
\(=(t_1+t_2)f(x_2)-f((t_1+t_2)x_2)\)
\(=f(x_2)-f(x_2)\)
\(=0\)
をとるので、\(F(x)≧0\)
したがって(A)が成り立つ。(等号成立は \((x=)\)\(x_1=x_2\) のとき)
(ii)\(n=k\) のとき (\(k=2,3,\cdots\))
\(t_1f(x_1)+t_2f(x_2)+\cdots+t_kf(x_k)≧f(t_1x_1+t_2x_2+\cdots+t_kx_k)\)
(\(t_1+t_2+\cdots+t_k=1\)、\(t_1,t_2,\cdots,t_k>0\))
(等号成立は \(x_1=x_2=\cdots=x_k\))
が成り立つと仮定する。
よって \(n=k+1\) でこの仮定を利用するために、無理やり\(k\)個になるようにまとめます。
このとき \(n=k+1\) では
(\(t_1+t_2+\cdots+t_k+t_{k+1}=1\)、\(t_1,t_2,\cdots,t_k,t_{k+1}>0\))
のもとで
\(\color{blue}{t_1f(x_1)+t_2f(x_2)}+t_3f(x_3)\cdots+t_kf(x_k)+t_{k+1}f(x_{k+1})\)
\(=\color{blue}{(t_1+t_2)\{\displaystyle\frac{t_1}{t_1+t_2}f(x_1)+\displaystyle\frac{t_2}{t_1+t_2}f(x_2)\}}+t_3f(x_3)+\cdots+t_kf(x_k)+t_{k+1}f(x_{k+1})\)
(\(n=2\) の不等式を使って)
\(≧\color{blue}{(t_1+t_2)\cdot f(\displaystyle\frac{t_1}{t_1+t_2}x_1+\displaystyle\frac{t_2}{t_1+t_2}x_2)}+t_3f(x_3)+\cdots+t_kf(x_k)+t_{k+1}f(x_{k+1})\)
(\(k\)個の和になっているので、\(n=k\) の仮定を使って)
\(≧ f\{(t_1+t_2)\cdot(\displaystyle\frac{t_1}{t_1+t_2}x_1+\displaystyle\frac{t_2}{t_1+t_2}x_2)+t_3x_3+\cdots+t_kx_k+t_{k+1}x_{k+1}\}\)
\(=f(t_1x_1+t_2x_2+\cdots+t_kx_k+t_{k+1}x_{k+1})\)
よって \(n=k+1\) のときも不等式は成り立つ。
等号成立は
\(n=2\) を利用した不等号で \(x_1=x_2\)・・・(ア)
\(n=k\) を利用した不等号で
\(\displaystyle\frac{t_1}{t_1+t_2}x_1+\displaystyle\frac{t_2}{t_1+t_2}x_2=x_3=\cdots=x_k=x_{k+1}\)・・・(イ)
(ア)を(イ)に代入して
\(\displaystyle\frac{t_1+t_2}{t_1+t_2}x_1=x_3=\cdots=x_k=x_{k+1}\)
したがって
\(x_1=x_2=x_3=\cdots=x_k=x_{k+1}\)
となり、等号成立についても \(n=k+1\) でも成り立つ。
(証明2)接線と凸関数の位置関係
(下に凸の場合、接線は下側にあることを利用します。こちらは和をシグマで表したいと思います。証明1でもシグマを使っても構いません)
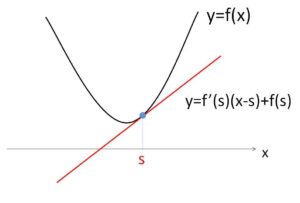
\(f”(x)>0\) のとき
\(f(x)≧f'(s)(x-s)+f(s)\)・・・(a) (\(x=s\)のとき等号成立)
が成り立つ。
\(s=\displaystyle\sum_{k=1}^{n}t_kx_k\) とおくと (示したい右辺の関数の中身を\(s\)にする)
(a)で
\(x=x_1\) を代入して\(t_1\)倍
\(x=x_2\) を代入して\(t_2\)倍
・・・
\(x=x_n\) を代入して\(t_n\)倍
した不等式を辺々加えると
\(\displaystyle\sum_{k=1}^{n}t_kf(x_k)\)\(≧\displaystyle\sum_{k=1}^{n}t_k\{f'(s)(x_k-s)+f(s)\}\)
\(=f'(s)(\displaystyle\sum_{k=1}^{n}t_kx_k-s\displaystyle\sum_{k=1}^{n}t_k)+f(s)\displaystyle\sum_{k=1}^{n}t_k\)
\(=f'(s)(s-s)+f(s)\)
\(=f(s)\)
\(=f(\displaystyle\sum_{k=1}^{n}t_kx_k)\)
等号は
\(x_1=x_2=\cdots=x_n\)\((=s)\)
のとき成立。
・凸関数と多角形
イェンゼンの不等式でよく利用するのは、\(n=2,3\) の場合です。
\(n=2\) の場合は、線分の内分点が関数の上側(下側)にあるというのは今まで扱ってきた通りです。
\(n=3\) の場合で、とくに \(t_1=t_2=t_3=\displaystyle\frac{1}{3}\) とすると、\(f”(x)>0\) のとき
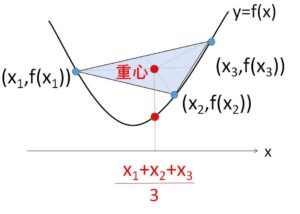
\(\displaystyle\frac{f(x_1)+f(x_2)+f(x_3)}{3}≧f(\displaystyle\frac{x_1+x_2+x_3}{3})\)
となりますが、これは3点 \((x_1,f(x_1))\)、\((x_2,f(x_2))\)、\((x_3,f(x_3))\) を頂点とする三角形を考えると、
(三角形の重心の\(y\)座標)≧(\(f\)(三角形の重心の\(x\)座標))
という図形的意味をもちます。
\(n=3\) で \(t_1,t_2,t_3\) が他の値のときも、\((x_1,f(x_1))\)、\((x_2,f(x_2))\) の内分点
\((\displaystyle\frac{t_1x_1+t_2x_2}{t_2+t_1},\displaystyle\frac{t_1f(x_1)+t_2f(x_2)}{t_2+t_1})\)
を考えて、さらにこの点と \((x_3,f(x_3))\) の内分点
\(\left(\displaystyle\frac{(t_1+t_2)\cdot\displaystyle\frac{t_1x_1+t_2x_2}{t_2+t_1}+t_3x_3}{t_3+(t_1+t_2)},\displaystyle\frac{(t_1+t_2)\cdot\displaystyle\frac{t_1f(x_1)+t_2f(x_2)}{t_2+t_1}+t_3f(x_3)}{t_3+(t_1+t_2)}\right)\)
\(=(t_1x_1+t_2x_2+t_3x_3,t_1f(x_1)+t_2f(x_2)+t_3f(x_3))\)・・・(※)
を考えることで、イェンゼンの不等式
\(t_1f(x_1)+t_2f(x_2)+t_3f(x_3)≧f(t_1x_1+t_2x_2+t_3x_3)\)
より、(※)の点が関数の上側にあるのはもちろん、三角形の内側にあることも分かります。
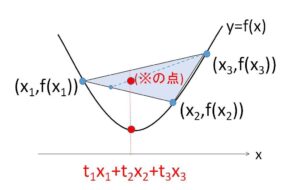
このことを拡張すると(帰納法で示せる)、\(n\) (\(n≧3\)) の場合のイェンゼンの不等式は
点\((t_1x_1+t_2x_2+\cdots+t_nx_n,\ t_1f(x_1)+t_2f(x_2)+\cdots+t_nf(x_n))\)
が関数の上側にあることを意味しているのはもちろんですが、さらにこの点が\(n\)角形の内側に位置していることになります。
長くなったので演習は次回に回します。
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→凸関数(演習) back→凸関数①