接線の本数に関する例題です。
そして、\(t\)に関する方程式を立てて、\(t\)の実数解の個数を数えます。
その際\(t\)が異なれば、接線は異なるかどうかには気を配ります。
(例題)
関数 \(y=(\log x)^2\) について、以下の問いに答えよ。
(1)関数 \(y=(\log x)^2\) の増減、極値、グラフの凹凸と変曲点を調べて、そのグラフをかけ。
(2)関数 \(y=(\log x)^2\) のグラフ上の 点\((t,(\log t)^2)\) を通る接線が 点\(A(0,a)\) を通るとき\(a\)を\(t\)を用いて表せ。
(3)点\(A(0,a)\) から関数 \(y=(\log x)^2\) のグラフへ異なる2本の接線が引けるような\(a\)の値の範囲を求めよ。
(4)\(a\)が(3)で求めた範囲の値をとるとき、点\(A(0,a)\) から関数 \(y=(\log x)^2\) のグラフへ引いた異なる2本の接線が直交するような\(a\)の値を求めよ。
(解答)
(1)
\(y=(\log x)^2\) (\(x>0\))
\(y’=2(\log x)\cdot\displaystyle\frac{1}{x}=\displaystyle\frac{2\log x}{x}\)
(\(y’=0\) を満たすのは \(x=1\))
\(y”=2\cdot\displaystyle\frac{\displaystyle\frac{1}{x}\cdot x-\log x\cdot1}{x^2}\)
\(=\displaystyle\frac{2(1-\log x)}{x^2}\)
(\(y”=0\) を満たすのは \(x=e\))
また
\(\displaystyle\lim_{x \to +0}(\log x)^2=\infty\)
\(\displaystyle\lim_{x \to \infty}(\log x)^2=\infty\)
だから、増減表とグラフは次の通り。
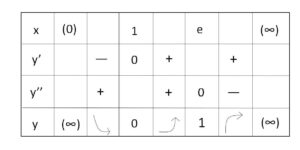
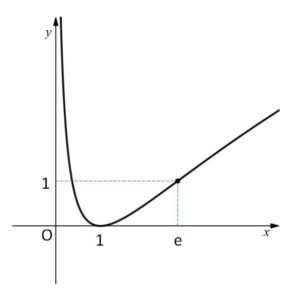
変曲点は \((e,1)\)
(2)
\(y’=\displaystyle\frac{2\log x}{x}\) より
\((t,(\log t)^2)\) における接線の方程式は
\(y=\displaystyle\frac{2\log t}{t}(x-t)+(\log t)^2\)
この接線は \((0,a)\) を通るから
\(a=-2\log t+(\log t)^2\)
(3)
「(接線の本数)=(接点の個数)」
となるので、(2)で求めた方程式
\(a=-2\log t+(\log t)^2\)
が、異なる2つの実数解\(t\)をもつ条件を調べます。定数分離によって、右辺の関数の増減を調べてもよいですが、\(\log t\)の2次方程式であることに着目すると楽です。
なお(注)については今回はグラフより判断したいと思います。詳しくは後述します。
\(y=(\log x)^2\) のグラフより、接点の\(x\)座標が異なれば接線は異なるので、
点\(A(0,a)\) から異なる2本の接線が引ける条件は
(2)で求めた\(t\)の方程式
\((\log t)^2-2\log t-a=0\)
\(\log t=X\) とおくと、\(X\)はすべての実数をとりうるので
\(X^2-2X-a=0\)
について判別式より
\(\displaystyle\frac{D}{4}=1+a>0\)
よって \(a>-1\)
(注)
ある点における接線が、他の点でも接するとき(2重接線のような場合)
「(接線の本数)≠(接点の個数)」 となってしまうので、接点が異なれば接線が異なることの確認が必要です。確認には
(i)傾きや切片の増減を調べる(単調増加(減少)が言えればよい)
(ii)グラフの形状で考える(増減や凸性)
などの方法があります。本問では(i)の方法だと
傾き:\(F(t)=\displaystyle\frac{2\log t}{t}\)
\(y\)切片:\(G(t)=-2\log t+(\log t)^2\)
がどちらも単調関数ではないので、(i)の方法ではうまくいきません。
そこで(ii)の方法をとると、\(x=e\) で \(y=(\log x)^2\) のグラフの凸性が変わることに着目すると、変曲点を \(P(e,1)\) として
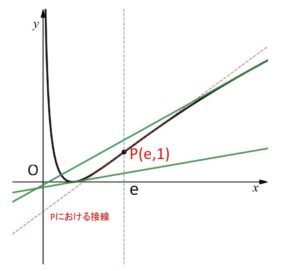
\(0<x<e\) での接線は、\(x=e\) において\(P\)の下側を通る。
\(x>e\) での接線は、\(x=e\) において\(P\)の上側を通る。
(また、凸性が同じところでは2点以上で接することはない)
ことから、接点が異なると接線が異なることが分かります。
(4)
これに気づかない場合でも、解く方法はあります。(別解)
なお直交条件はもちろん (傾きの積)=-1 を用います。
2本の接線の接点の座標を \(t=α,β\) (\(α≠β\)) とおくと
\((\log t)^2-2\log t-a=0\)
の2解が \(t=α,β\) である。よって解と係数の関係から
\(\logα+\logβ=2\)・・・①
\((\logα)(\logβ)=-a\)・・・②
2本の接線は直交するから \(y’=\displaystyle\frac{2\log x}{x}\) より
\(\displaystyle\frac{2\logα}{α}\cdot\displaystyle\frac{2\logβ}{β}=-1\)・・・③
①より
\(\logαβ=2\) だから
\(αβ=e^2\)
よってこれと②を③に代入して
\(\displaystyle\frac{-4a}{e^2}=-1\)
したがって
\(a=\displaystyle\frac{e^2}{4}\) (\(a>-1\) を満たす)
(別解)
2本の接線の接点の座標を \(t=α,β\) (\(α≠β\)) とおくと
\(a=-2\log t+(\log t)^2\)
に \(t=α,β\) を代入すると成り立つので
\(-2\logα+(\logα)^2=a\)・・・④
\(-2\logβ+(\logβ)^2=a\)・・・⑤
また2本の接線が直交するから
\(\displaystyle\frac{4(\logα)(\logβ)}{αβ}=-1\)・・・③
(最終的に\(α,β\)を消去していきます)
④-⑤より
\(-2(\logα-\logβ)+(\logα)^2-(\logβ)^2=0\)
\((\logα-\logβ)(-2+\logα+\logβ)=0\)
\(α≠β\) だから
\(\logα+\logβ=2\)
\(\logαβ=2\)
\(αβ=e^2\)
これを③に代入して
\(\displaystyle\frac{4(\logα)(\log\displaystyle\frac{e^2}{α})}{e^2}=-1\)
\((\logα)(2-\logα)=-\displaystyle\frac{e^2}{4}\)
\(2\logα-(\logα)^2=-\displaystyle\frac{e^2}{4}\)
④より
\(-a=-\displaystyle\frac{e^2}{4}\)
したがって
\(a=\displaystyle\frac{e^2}{4}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→同形出現と微分 back→方程式の解の個数