微小変化量

微小変化量について見ていきます。

・微小変化量
\(x\)の増分\(Δx\)に対する、\(y\)の増分を\(Δy\)とすると、微分の定義

\(\displaystyle\lim_{Δx \to 0}\displaystyle\frac{Δy}{Δx}=y’\)

より、\(Δx\)が\(0\)に近いとき

\(\displaystyle\frac{Δy}{Δx}≒y’\)

と近似できるので、微小変化量\(Δy\)を次のように近似することができます。

\(Δy≒y’Δx\)・・・(i)

(\(y’\)は変化させる前の微分係数)

なお(i)は前回やった
\(f(a+h)≒f(a)+f'(a)h\)・・・①
\(f(x)≒f(a)+f'(a)(x-a)\)・・・②

と本質的には同じ近似式です。いずれも微分の定義を出発点としていることからも分かりますし、①で \(h=x-a\) とすると②になるので①と②は同じ式で、また①より
\(f(a+h)-f(a)≒f'(a)h\)
であり、 \(h=Δx\) とすると、\(y=f(x)\) において \(f(a+Δx)-f(a)=Δy\) となるので
\(Δy≒y’Δx\)
となり(i)が導けます。

(例題)
2辺がそれぞれ\(3cm\)、\(4cm\)で、その間の角が\(30°\)の三角形がある。2辺の長さはそのままで、間の角を\(1°\)増やすと、その面積は約何\(cm^2\)変化するか。1次近似式を利用して小数第2位まで求めよ。ただし \(\sqrt{3}=1.73\)、\(π=3.14\) とする。

(解答)

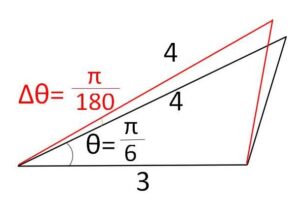
間の角を\(θ\)とすると、その面積\(S(θ)\)は
\(S(θ)=\displaystyle\frac{1}{2}\cdot4\cdot3\sinθ\)\(=6\sinθ\)

\(θ\)の増分\(Δθ\)に対する\(S(θ)\)の増分を\(ΔS\)とすると、\(Δθ\)が微小なとき
\(ΔS≒S'(θ)Δθ\)
が成り立つ。

\(θ=\displaystyle\frac{π}{6}\)、\(Δθ=\displaystyle\frac{π}{180}\)、\(S'(θ)=6\cosθ\) より

\(ΔS≒6\cos\displaystyle\frac{π}{6}\cdot(\displaystyle\frac{π}{180})\)

\(=3\sqrt{3}\cdot\displaystyle\frac{π}{180}\)

\(=\displaystyle\frac{1.73×3.14}{60}\)

\(≒0.09\)

よって約\(0.09cm^2\) 増える。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→2次以上の近似式　back→1次近似式