複素数平面と共役複素数

共役複素数と複素数平面の関係や、複素数の演算について見ていきます。

・共役複素数と複素数平面
複素数 \(z=x+yi\) について虚部の符号を変えた複素数を共役な複素数とよび \(\bar{z}\) で表します。つまり
\(\bar{z}=\overline{x+yi}=x-yi\)
です。なお例えば実数 \(z=3\) の共役な複素数は \(z=3+0i\) より
\(\bar{z}=3-0i=3\)
となり、もとの複素数と同じになります。

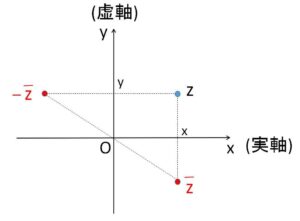
共役な複素数ともとの複素数は虚部の符号が違うだけなので、複素数平面で図示すると実軸について対称な位置関係になります。またある複素数を\(-1\)倍すると原点について対称な位置に移動するので、\(z\)と\(-\bar{z}\)は虚軸について対称な位置関係になります。

これらのことから共役な複素数を利用する、\(z\)の実数判定や純虚数判定が可能になりますがこれは次回に扱いたいと思います。

・共役複素数の演算
共役な複素数の演算について、次のことが成り立ちます。

(1)\(\overline{α+β}=\bar{α}+\bar{β}\)
(2)\(\overline{α-β}=\bar{α}-\bar{β}\)
一般的には
\(\overline{α_1±α_2±\cdots±α_{n}}=\overline{α_1}±\overline{α_2}±\cdots±\overline{α_n}\)

(3)\(\overline{αβ}=\overline{α}\cdot\overline{β}\)
特に \(\overline{α^2}=(\overline{α})^2\)
一般的には
\(\overline{α_1α_2\cdots α_n}=\overline{α_1}\cdot\overline{α_2}\cdots\overline{α_n}\)
\(\overline{α^n}=(\overline{α})^n\)

(4)\(\overline{\left(\displaystyle\frac{α}{β}\right)}=\ \displaystyle\frac{\bar{α}}{\bar{β}}\)　(ただし \(β≠0\))

(5)\(\overline{\overline{α}}=α\)

(解説)
(1)~(4)は要するに、バラバラに共役複素数をとってもよいということです。(5)は2回共役な複素数をとると元に戻るということです。証明は \(α=a+bi\)、\(β=c+di\) とおけばすべて示せます。(\(n\)個の和・差、積については数学的帰納法を使う)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→実数・純虚数条件　back→複素数平面と平行移動