複素数平面における分点と三角形の重心の求め方です。
・内分点・外分点(複素数平面)
座標平面やベクトルと同様に、複素数平面においても線分の内分・外分点で同様の公式が成り立ちます。
2点 \(A(α), B(β)\)を結ぶ線分を \(m:n\) (\(m,n\)は正の数) に
内分する点を表す複素数は \(\displaystyle\frac{nα+mβ}{m+n}\)
とくに中点を表す複素数は \(\displaystyle\frac{α+β}{2}\)
外分する点を表す複素数は \(\displaystyle\frac{-nα+mβ}{m-n}\)
(証明)
座標平面で考えればすぐに分かる。内分点だけを示しておくと
\(α=a+bi\)、\(β=c+di\)
とおいて、内分点\(Z\)を表す複素数を \(z=x+yi\) とすると
\(A(a,b)\)、\(B(c,d)\)、\(Z(x,y)\) に対応するから
\(x=\displaystyle\frac{na+mc}{m+n}\)
\(y=\displaystyle\frac{nb+md}{m+n}\)
したがって
\(z=\displaystyle\frac{na+mc}{m+n}+\displaystyle\frac{nb+md}{m+n}i\)
\(=\displaystyle\frac{n(a+bi)+m(c+di)}{m+n}\)
\(=\displaystyle\frac{nα+mβ}{m+n}\)
なお、\(α\)がベクトル\(\overrightarrow{OA}\)を表す複素数であることに着目すると、位置ベクトルにより \(A(\vec{a}),B(\vec{b}),Z(\vec{z})\) で表すと
\(\vec{z}=\displaystyle\frac{n\vec{a}+m\vec{b}}{m+n}\)
であり、上記公式はこれに対応しています。
・三角形の重心(複素数平面)
\(A(α),B(β),C(γ)\)を頂点とする\(△ABC\)の重心を表す複素数は
\(\displaystyle\frac{α+β+γ}{3}\)
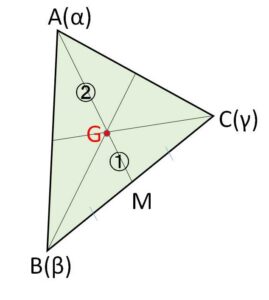
(証明)
同様に座標平面で考えてもよいですが、せっかくなので上記分点の公式から導いて見ます。
\(BC\)の中点\(M\)を表す複素数は \(\displaystyle\frac{β+γ}{2}\) なので、重心\(G\)は\(AM\)を\(2:1\)に内分する点だから、重心を表す複素数は
\(\displaystyle\frac{1\cdotα+2\cdot\displaystyle\frac{β+γ}{2}}{2+1}\)
\(=\displaystyle\frac{α+β+γ}{3}\)
なおこれも \(A(\vec{a})、B(\vec{b})、C(\vec{c})、G(\vec{g})\) とおくと
\(\vec{g}=\displaystyle\frac{\vec{a}+\vec{b}+\vec{c}}{3}\)
に対応しています。
(例題)
3点 \(A(5+4i),B(3-2i),C(1+2i)\) を頂点とする三角形\(ABC\)の重心を表す複素数\(δ\)を求めよ。
(解答)
\(δ=\displaystyle\frac{(5+4i)+(3-2i)+(1+2i)}{3}\)
\(=3+\displaystyle\frac{4}{3}i\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→なす角と複素数 back→ド・モアブルの定理と三角関数の等式の証明