複素数平面の領域についてです。
・複素数平面と領域
複素数平面の領域に関する問題では色々な解法がありますが、まずは基本となる形式(円・二等分線)をおさえておきます。
(円の内部)
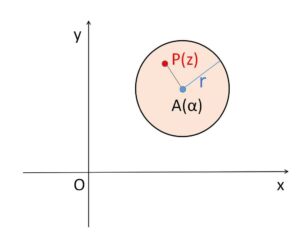
中心\(A(α)\)、半径\(r\)の円周およびその内部を表す不等式は、\(P(z)\)とおくと \(AP≦r\) より次のようになります。
\(|z-α|≦r\)
不等号の=がつかない場合には円の内部(円周上を含まない)となります。
(垂直二等分線の片側)
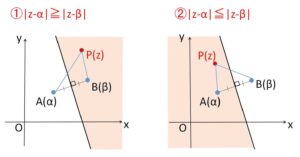
次の不等式
①\(|z-α|≧|z-β|\)
②\(|z-α|≦|z-β|\)
で表される領域はそれぞれ、上図のような垂直二等分線上とそれにより分けられた領域の片側になります。\(P(z),A(α),B(β)\) とすると
①は \(PA≧PB\)、②は\(PA≦PB\)
となることから分かります。または①②の両辺を2乗して \(z=x+yi\) とおいても調べることができます。
(例題1)
複素数\(z\)が
\(|z-1|≦|z|≦1\)
を満たしている。このとき複素数平面上で点\(z\)の動く範囲を図示せよ。
(解答)
\(|z|≦1\) は、中心を原点とする半径\(1\)の円周及び内部を表す。
\(|z|≧|z-1|\) は、2点\(0,1\) を結ぶ線分の垂直2等分線上と、これによって分けられる領域の右側を表す。よって、これらの共通部分が動く範囲で図示すると次の通り。
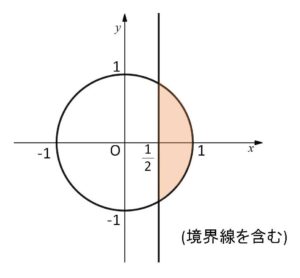
(参考)
\(|z-1|≦|z|\) については、次のように考えてもよいです。
\(|z-1|^2≦|z|^2\) より
\(|z|^2-z-\bar{z}+1≦|z|^2\)
\(z+\bar{z}≧1\)・・・①
\(z=x+yi\) とおくと①より
\(2x≧1\)
\(x≧\displaystyle\frac{1}{2}\) (\(y\)は任意)
(例題2)
複素数\(z\)は、複素数平面上で原点を中心とする半径\(1\)の円の内部(円周上を含まない)を動く。このとき
\(w=\displaystyle\frac{2z-i}{2+iz}\)
を満たす点\(w\)の動く範囲を求めよ。
(解答)
条件より
\(|z|<1\)・・・①
また
\(w=\displaystyle\frac{2z-i}{2+iz}\) より
\(w(2+iz)=2z-i\)
\((iw-2)z=-2w-i\)・・・②
\(w=-2i\) は②を満たさないので、\(w≠-2i\) であり②より
\(z=\displaystyle\frac{-2w-i}{iw-2}\)・・・③
③を①に代入して
\(\left|\displaystyle\frac{-2w-i}{iw-2}\right|<1\)
\(|2w+i|<|iw-2|\)
2乗して
\((2w+i)(2\bar{w}-i)<(iw-2)(-i\bar{w}-2)\)
整理すると
\(3w\bar{w}<3\)
\(|w|^2<1\)
\(|w|<1\)
したがって\(w\)は原点を中心とする半径\(1\)の円の内部(円周上を含まない)を動く。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→複素数平面と領域②(x+yi型) back→複素数平面と軌跡②(x+yi型)