内積の図形的意味を利用する問題について見ていきます。
(例題1)
\(△ABC\)において、辺\(CA\)の垂直2等分線と辺\(CB\)の垂直2等分線の交点を\(P\)とし、\(\overrightarrow{CA}=\vec{a}\), \(\overrightarrow{CB}=\vec{b}\), \(\overrightarrow{CP}=\vec{p}\) とする。\(|\vec{a}|=2\), \(|\vec{b}|=4\), 内積 \(\vec{a}\cdot\vec{b}=6\) のとき、次の問いに答えよ。
(1)内積 \(\vec{a}\cdot\vec{p}\), \(\vec{b}\cdot\vec{p}\) を求めよ。
(2)\(\vec{p}=s\vec{a}+t\vec{b}\) をみたす\(s,t\)の値を求めよ。
式のみで処理するなら(2)の\(s,t\)を先に求める方法になります(別解)。
(解答)
(1)
なお解答にはさほど影響しませんが、条件より \(\vec{a},\vec{b}\) のなす角を\(θ\)とすると、\(\cosθ=\displaystyle\frac{6}{2\cdot4}=\displaystyle\frac{3}{4}\) なので、\(30°<θ<45°\) です。図示するときの目安にしてください。
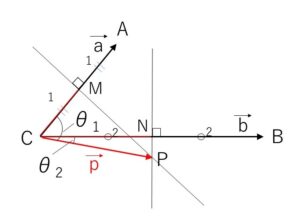
図より
\(\vec{a}\cdot\vec{p}=|\vec{a}||\vec{p}|\cosθ_1=CA×CM\)
\(=2×1\)\(=2\)
\(\vec{b}\cdot\vec{p}=|\vec{b}||\vec{p}|\cosθ_2=CB×CN\)
\(=4×2\)\(=8\)
(2)
なお、\(\vec{a},\vec{b}\)は\(\vec{0}\)でなく、平行でないので1次独立。よって\(s,t\)はただ1通り存在することになります。
\(\vec{p}=s\vec{a}+t\vec{b}\)
(1)より
\(\vec{a}\cdot\vec{p}=2\) だから
\(\vec{a}\cdot(s\vec{a}+t\vec{b})=2\)
\(s|\vec{a}|^2+t\vec{a}\cdot\vec{b}=2\)
よって
\(4s+6t=2\)・・・①
\(\vec{b}\cdot\vec{p}=8\) だから
\(\vec{b}\cdot(s\vec{a}+t\vec{b})=8\)
\(s\vec{a}\cdot\vec{b}+t|\vec{b}|^2=8\)
よって
\(6s+16t=8\)・・・②
①②より
\(s=-\displaystyle\frac{4}{7}\), \(t=\displaystyle\frac{5}{7}\)
(別解)(2)を先に解く
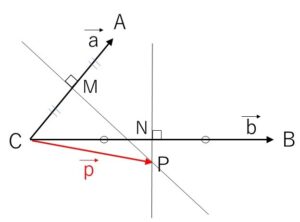
\(\overrightarrow{MP}=\overrightarrow{CP}-\overrightarrow{CM}\)
\(=s\vec{a}+t\vec{b}-\displaystyle\frac{1}{2}\vec{a}\)
\(=(s-\displaystyle\frac{1}{2})\vec{a}+t\vec{b}\)
\(CA \perp MP\) より
\(\vec{a}\cdot\{(s-\displaystyle\frac{1}{2})\vec{a}+t\vec{b}\}=0\)
展開すると
\(4s-2+6t=0\)・・・(i)
\(\overrightarrow{NP}=\overrightarrow{CP}-\overrightarrow{CN}\)
\(=s\vec{a}+t\vec{b}-\displaystyle\frac{1}{2}\vec{b}\)
\(=s\vec{a}+(t-\displaystyle\frac{1}{2})\vec{b}\)
\(CB \perp NP\) より
\(\vec{b}\cdot\{(s\vec{a}+(t-\displaystyle\frac{1}{2})\vec{b}\}=0\)
展開すると
\(6s+16t-8=0\)・・・(ii)
(i)(ii)より
\(s=-\displaystyle\frac{4}{7}\), \(t=\displaystyle\frac{5}{7}\)
また(1)については
\(\vec{a}\cdot\vec{p}=\vec{a}\cdot(-\displaystyle\frac{4}{7}\vec{a}+\displaystyle\frac{5}{7}\vec{b})\)
\(=-\displaystyle\frac{16}{7}+\displaystyle\frac{30}{7}\)
\(=2\)
\(\vec{b}\cdot\vec{p}=\vec{b}\cdot(-\displaystyle\frac{4}{7}\vec{a}+\displaystyle\frac{5}{7}\vec{b})\)
\(=-\displaystyle\frac{24}{7}+\displaystyle\frac{80}{7}\)
\(=8\)
(例題2)
(1)平面上に2点\(A,X\)がある。原点\(O\)と点\(A\)を通る直線に点\(X\)から下した垂線の足を\(H\)とする。\(\overrightarrow{OH}=t\overrightarrow{OA}\)と表すとき、
\(\overrightarrow{OA}\cdot\overrightarrow{OX}=\overrightarrow{OA}\cdot\overrightarrow{OH}=t|\overrightarrow{OA}|^2\) であることを示せ。
(2)平面上に点\(A(3,2)\)と、4点 \(P(-4,1)\), \(Q(-2,1)\), \(R(-2,3)\), \(S(-4,3)\) を頂点とする正方形がある。いま、動点\(X\)がこの正方形の辺上を1周するとき、\(\overrightarrow{OA}\cdot\overrightarrow{OX}\)のとり得る値の範囲を求めよ。
(解答)
(1)
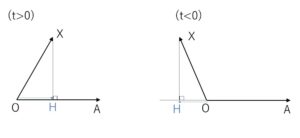
\(\overrightarrow{OA}\cdot\overrightarrow{OX}\)
\(=\overrightarrow{OA}\cdot(\overrightarrow{OH}+\overrightarrow{HX})\)
\(=\overrightarrow{OA}\cdot\overrightarrow{OH}+\overrightarrow{OA}\cdot\overrightarrow{HX}\)
\(=\overrightarrow{OA}\cdot\overrightarrow{OH}\) (\(∵\overrightarrow{OA}\perp\overrightarrow{HX}\))
\(=\overrightarrow{OA}\cdot t\overrightarrow{OA}\)
\(=t|\overrightarrow{OA}|^2\)
(2)
\(t\)の範囲は、\(\overrightarrow{OH}=t\overrightarrow{OA}\) より\(X\)から下した垂線の足の\(H\)がどの範囲にあるかによって決まるので、\(OA\)に垂直な直線を正方形と交わるように動かすことで\(H\)の範囲をとらえていきます。
なおこの問題も誘導を無視する別解があります。
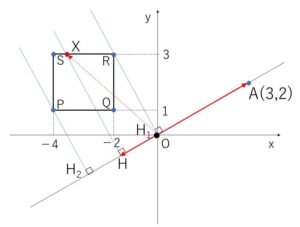
\(\overrightarrow{OA}\cdot\overrightarrow{OX}=t|\overrightarrow{OA}|^2\) より
\(t\)のとり得る範囲を調べればよい。
\(\overrightarrow{OH}=t\overrightarrow{OA}\) だから、\(X\)から下した垂線の足\(H\)の動く範囲を考えればよく、\(OA\)に垂直な直線が正方形と交わる場合を考えると、垂線の足\(H\)は図の\(H_1\)から\(H_2\)までの間を動く。
よって \(\overrightarrow{OA}\cdot\overrightarrow{OX}\) の最小値は \(H=H_2\) つまり \(X=P\) のときで
\(\overrightarrow{OA}\cdot\overrightarrow{OX}=(3,2)\cdot(-4,1)\)\(=-10\)
最大値は \(H=H_1\) つまり \(X=R\) のときで (このとき\(H_1\)は原点\(O\)になる)
\(\overrightarrow{OA}\cdot\overrightarrow{OX}=(3,2)\cdot(-2,3)\)\(=0\)
したがって
\(-10≦\overrightarrow{OA}\cdot\overrightarrow{OX}≦0\)
(別解)
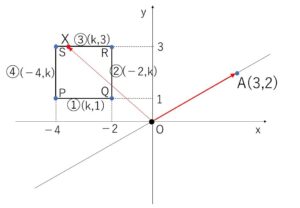
①\(X\)が\(PQ\)上にあるとき
\(X(k,1)\) (\(-4≦k≦-2\)) とおけて
\(\overrightarrow{OA}\cdot\overrightarrow{OX}=(3,2)\cdot(k,1)=3k+2\)
よって \(-10≦\overrightarrow{OA}\cdot\overrightarrow{OX}≦-4\)
②\(X\)が\(QR\)上にあるとき
\(X(-2,k)\) (\(1≦k≦3\)) とおけて
\(\overrightarrow{OA}\cdot\overrightarrow{OX}=(3,2)\cdot(-2,k)=-6+2k\)
よって \(-4≦\overrightarrow{OA}\cdot\overrightarrow{OX}≦0\)
③\(X\)が\(RS\)上にあるとき
\(X(k,3)\) (\(-4≦k≦-2\)) とおけて
\(\overrightarrow{OA}\cdot\overrightarrow{OX}=(3,2)\cdot(k,3)=3k+6\)
よって \(-6≦\overrightarrow{OA}\cdot\overrightarrow{OX}≦0\)
④\(X\)が\(SP\)上にあるとき
\(X(-4,k)\) (\(1≦k≦3\)) とおけて
\(\overrightarrow{OA}\cdot\overrightarrow{OX}=(3,2)\cdot(-4,k)=-12+2k\)
よって \(-10≦\overrightarrow{OA}\cdot\overrightarrow{OX}≦-6\)
以上から
\(-10≦\overrightarrow{OA}\cdot\overrightarrow{OX}≦0\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→内積の図形的意味② back→正五角形とベクトル