成分表示したときの内積について見ていきます。
・成分表示による内積
\(\vec{a}=(a_1,a_2)\), \(\vec{b}=(b_1,b_2)\) のとき、内積 \(\vec{a}\cdot\vec{b}\) は次の簡単な式で計算することができます。
\(\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2\)
証明は、\(|\vec{a}|,|\vec{b}|\)を2辺、挟む角を\(θ\)とする三角形について余弦定理を考えます。すると \(|\vec{a}||\vec{b}|\cosθ\) の項が出てきます。
(証明)
(i)\(\vec{a}≠\vec{0}\), \(\vec{b}≠\vec{0}\) のとき
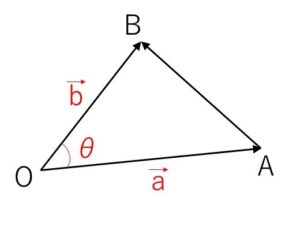
\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\), \(\angle AOB=θ\) とする。
\(0°<θ<180°\) のとき \(△OAB\)が存在するので、余弦定理より
\(AB^2=OA^2+OB^2-2OA\cdot OB\cosθ\)・・・①
(この等式は、\(θ=0°,180°\) でも成り立つ)
①より
\(2\vec{a}\cdot\vec{b}=OA^2+OB^2-AB^2\)
\(\overrightarrow{AB}=(b_1-a_1,b_2-a_2)\) だから
\(2\vec{a}\cdot\vec{b}=(a_1^2+a_2^2)+(b_1^2+b_2^2)-\{(b_1-a_1)^2+(b_2-a_2)^2\}\)
よって
\(2\vec{a}\cdot\vec{b}=2a_1b_1+2a_2b_2\)
\(\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2\)・・・②
(ii)\(\vec{a}=\vec{0}\) または \(\vec{b}=\vec{0}\) のとき
②の両辺が\(0\)となるので、このときも成立
大きさも、\(|\vec{a}|=\sqrt{a_1^2+a_2^2}\), \(|\vec{b}|=\sqrt{b_1^2+b_2^2}\) と計算できるので、成分が分かると \(\cosθ\)、つまりなす角が分かることになります(特に\(30°\)などの有名角)。
・成分表示と垂直・平行
\(\vec{a}=(a_1,a_2)\), \(\vec{b}=(b_1,b_2)\) (\(\vec{a}≠\vec{0}\), \(\vec{b}≠\vec{0}\)) のとき、ベクトルの垂直・平行について次のことが成り立ちます。
(垂直条件): \(\vec{a}\perp\vec{b}\) \(⇔\) \(a_1b_1+a_2b_2=0\)
(平行条件): \(\vec{a}/\!/\vec{b}\) \(⇔\) \(a_1b_2-a_2b_1=0\)
(証明)
垂直については
\(\vec{a}\perp\vec{b}\) \(⇔\) なす角が\(90°\) \(⇔\) \(\vec{a}\cdot\vec{b}=0\) \(⇔\) \(a_1b_1+a_2b_2=0\)
平行についての条件は新しい知識ではないが、内積を利用して証明すると
\(\vec{a}/\!/\vec{b}\) \(⇔\) なす角が\(0°\) or \(180°\) \(⇔\) \(\vec{a}\cdot\vec{b}=±|\vec{a}||\vec{b}|\) \(⇔\) \((\vec{a}\cdot\vec{b})^2=(|\vec{a}||\vec{b}|)^2\)
最後の等式を成分表示を用いて計算すると
\((a_1b_1+a_2b_2)^2=(a_1^2+a_2^2)(b_1^2+b_2^2)\)
整理して
\(a_1^2b_2^2-2a_1a_2b_1b_2+a_2^2b_1^2=0\)
\((a_1b_2-a_2b_1)^2=0\)
\(⇔\) \(a_1b_2-a_2b_1=0\)
・内積の演算
普通の数(スカラー)と同様に、内積について次の法則が成り立ちます。
(1)\(\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}\) (交換法則)
(2)\((\vec{a}+\vec{b})\cdot\vec{c}=\vec{a}\cdot\vec{c}+\vec{b}\cdot\vec{c}\) (分配法則)
(\(\vec{a}\cdot(\vec{b}+\vec{c})=\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}\))
(3)\((k\vec{a})\cdot\vec{b}=\vec{a}\cdot(k\vec{b})=k(\vec{a}\cdot\vec{b})\) \((=k\vec{a}\cdot\vec{b})\) (\(k\)は実数)
すべて成分表示を用いて証明できます。(1)については内積の定義を考えてもよいです。
例えば(2)の
「\((\vec{a}+\vec{b})\cdot\vec{c}=\vec{a}\cdot\vec{c}+\vec{b}\cdot\vec{c}\) 」の証明だと
\(\vec{a}=(a_1,a_2)\), \(\vec{b}=(b_1,b_2)\), \(\vec{c}=(c_1,c_2)\) おくと
(左辺)
\(=(a_1+b_1,a_2+b_2)\cdot(c_1,c_2)\)
\(=(a_1+b_1)c_1+(a_2+b_2)c_2\)
\(=a_1c_1+b_1c_1+a_2c_2+b_2c_2\)
(右辺)
\(=(a_1,a_2)\cdot(c_1,c_2)+(b_1,b_2)\cdot(c_1,c_2)\)
\(=a_1c_1+a_2c_2+b_1c_1+b_2c_2\)
よって (左辺)=(右辺)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→内積の計算 back→内積の定義