引き続き、内積とベクトルの大きさに関する演習です。
(例題1)
\(\vec{0}\) でない2つのベクトル\(\vec{a}\)と\(\vec{b}\)において、\(\vec{a}+2\vec{b}\) と \(\vec{a}-2\vec{b}\) が垂直で、\(|\vec{a}+2\vec{b}|=2|\vec{b}|\) とする。
(1)\(\vec{a}\) と \(\vec{b}\) のなす角\(θ\) (\(0°≦θ≦180°\)) を求めよ。
(2)\(|\vec{a}|=1\) のとき、\(|t\vec{a}+\displaystyle\frac{1}{t}\vec{b}|\) (\(t>0\)) の最小値を求めよ。
(解答)
(1)
\(\vec{a}+2\vec{b}\) と \(\vec{a}-2\vec{b}\) が垂直だから
\((\vec{a}+2\vec{b})\cdot(\vec{a}-2\vec{b})=0\)
\(|\vec{a}|^2-4|\vec{b}|^2=0\)
\(|\vec{a}|^2=4|\vec{b}|^2\)
\(|\vec{a}|>0\), \(|\vec{b}|>0\) より
\(|\vec{a}|=2|\vec{b}|\)・・・①
\(|\vec{a}+2\vec{b}|=2|\vec{b}|\) より
\(|\vec{a}+2\vec{b}|^2=4|\vec{b}|^2\)
\(|\vec{a}|^2+4\vec{a}\cdot\vec{b}+4|\vec{b}|^2=4|\vec{b}|^2\)
\(\vec{a}\cdot\vec{b}=-\displaystyle\frac{1}{4}|\vec{a}|^2\)・・・②
①②より
\(\cosθ=\displaystyle\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}=\displaystyle\frac{-\displaystyle\frac{1}{4}|\vec{a}|^2}{|\vec{a}|\cdot\displaystyle\frac{1}{2}|\vec{a}|}=-\displaystyle\frac{1}{2}\)
よって
\(θ=120°\)
(2)
\(|t\vec{a}+\displaystyle\frac{1}{t}\vec{b}|≧0\) より、\(|t\vec{a}+\displaystyle\frac{1}{t}\vec{b}|^2\) の最小値を考えればよい。
\(|\vec{a}|=1\) と (1)の①②より
\(|\vec{b}|=\displaystyle\frac{1}{2}\), \(\vec{a}\cdot\vec{b}=-\displaystyle\frac{1}{4}\) だから
\(|t\vec{a}+\displaystyle\frac{1}{t}\vec{b}|^2\)
\(=t^2|\vec{a}|^2+2\vec{a}\cdot\vec{b}+\displaystyle\frac{1}{t^2}|\vec{b}|^2\)
\(=t^2+\displaystyle\frac{1}{4t^2}-\displaystyle\frac{1}{2}\)
ここで、\(t>0\) より \(t^2>0\), \(\displaystyle\frac{1}{4t^2}>0\) だから
\(t^2+\displaystyle\frac{1}{4t^2}≧2\sqrt{t^2\cdot\displaystyle\frac{1}{4t^2}}=1\)
よって
\(|t\vec{a}+\displaystyle\frac{1}{t}\vec{b}|^2≧1-\displaystyle\frac{1}{2}=\displaystyle\frac{1}{2}\)
等号は、\(t^2=\displaystyle\frac{1}{4t^2}\) のときで、\(4t^4=1\) つまり \(t=\displaystyle\frac{1}{\sqrt{2}}\) のとき成立
したがって \(|t\vec{a}+\displaystyle\frac{1}{t}\vec{b}|^2\) の最小値は \(\displaystyle\frac{1}{2}\) だから
\(|t\vec{a}+\displaystyle\frac{1}{t}\vec{b}|\) の最小値は \(\displaystyle\frac{1}{\sqrt{2}}\) (このとき \(t=\displaystyle\frac{1}{\sqrt{2}}\))
(例題2)
平面上のベクトル \(\vec{a},\vec{b}\) が
\(|\vec{a}+2\vec{b}|=1\), \(|2\vec{a}-\vec{b}|=1\)
をみたすように動く。
(1)\(|\vec{a}+\vec{b}|\) の最大値と、そのときの \(|\vec{a}|,|\vec{b}|\) の値を求めよ。
(2)\(|\vec{a}+\vec{b}|\) の最小値と、そのときの \(|\vec{a}|,|\vec{b}|\) の値を求めよ。
\(|\vec{a}|^2+4\vec{a}\cdot\vec{b}+4|\vec{b}|^2=1\)
\(4|\vec{a}|^2-4\vec{a}\cdot\vec{b}+|\vec{b}|^2=1\)
となりますが、内積もベクトルの大きさに依存するのでさらに式変形すると
\(|\vec{a}|^2+4|\vec{a}||\vec{b}|\cosθ+4|\vec{b}|^2=1\)
\(4|\vec{a}|^2-4|\vec{a}||\vec{b}|\cosθ+|\vec{b}|^2=1\)
となり、理屈上は式2つで変数は \(|\vec{a}|,|\vec{b}|,\cosθ\) の3つなので2文字消去できて、\(|\vec{a}+\vec{b}|\) は実質1変数の関数となるわけですが、これだと大変です。
したがって別の方法に頼ることになりますが、条件式をよく見るとどちらもベクトルの大きさが1になっているので、左辺の中身全体を1つのベクトルとしてみると、これは原点を始点とすれば、終点が原点を中心とする円(単位円)上の点であるベクトルです。
(解答)
(1)(2)
\(\vec{a}+2\vec{b}=\vec{p}\)・・・①
\(2\vec{a}-\vec{b}=\vec{q}\)・・・②
とすると、条件式は
\(|\vec{p}|=1\), \(|\vec{q}|=1\)
①②から連立方程式を解く要領で、\(\vec{a}=(\vec{p},\vec{q}の式)\), \(\vec{b}=(\vec{p},\vec{q}の式)\) にします。
①+②×2 より
\(5\vec{a}=\vec{p}+2\vec{q}\)
\(\vec{a}=\displaystyle\frac{1}{5}(\vec{p}+2\vec{q})\)・・・③
①×2-② より
\(5\vec{b}=2\vec{p}-\vec{q}\)
\(\vec{b}=\displaystyle\frac{1}{5}(2\vec{p}-\vec{q})\)・・・④
よって
\(|\vec{a}+\vec{b}|\)
\(=|\displaystyle\frac{1}{5}(\vec{p}+2\vec{q})+\displaystyle\frac{1}{5}(2\vec{p}-\vec{q})|\)
\(=|\displaystyle\frac{3}{5}\vec{p}+\displaystyle\frac{1}{5}\vec{q}|\)
解答では、\(|\displaystyle\frac{3}{5}\vec{p}+\displaystyle\frac{1}{5}\vec{q}|^2\) を考えていきますが、不等式(三角不等式)を使ったりする方法もあります
ここで
\(|\displaystyle\frac{3}{5}\vec{p}+\displaystyle\frac{1}{5}\vec{q}|^2\)
\(=\displaystyle\frac{9}{25}|\vec{p}|^2+\displaystyle\frac{6}{25}\vec{p}\cdot\vec{q}+\displaystyle\frac{1}{25}|\vec{q}|^2\)
\(=\displaystyle\frac{9}{25}+\displaystyle\frac{6}{25}|\vec{p}||\vec{q}|\cos\phi+\displaystyle\frac{1}{25}\)
\(=\displaystyle\frac{10}{25}+\displaystyle\frac{6}{25}\cos\phi\) (\(\phi\)は\(\vec{p},\vec{q}\)のなす角)
\(-1≦\cos\phi≦1\) より・・・(注)
\(|\displaystyle\frac{3}{5}\vec{p}+\displaystyle\frac{1}{5}\vec{q}|^2\) の
最大値 \(\displaystyle\frac{10}{25}+\displaystyle\frac{6}{25}=\displaystyle\frac{16}{25}\) (\(\phi=0°\))
最小値 \(\displaystyle\frac{10}{25}-\displaystyle\frac{6}{25}=\displaystyle\frac{4}{25}\) (\(\phi=180°\))
よって\(|\vec{a}+\vec{b}|\) の最大値は \(\displaystyle\frac{4}{5}\) で
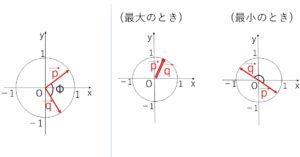
このとき、\(\vec{p},\vec{q}\) の向きが同じであることと、大きさがどちらも1であることから
\(\vec{p}=\vec{q}\)
③④より
\(\vec{a}=\displaystyle\frac{1}{5}(\vec{p}+2\vec{p})=\displaystyle\frac{3}{5}\vec{p}\)
\(\vec{b}=\displaystyle\frac{1}{5}(2\vec{p}-\vec{p})=\displaystyle\frac{1}{5}\vec{p}\)
であるから、\(|\vec{a}|=\displaystyle\frac{3}{5}\), \(|\vec{b}|=\displaystyle\frac{1}{5}\)
\(|\vec{a}+\vec{b}|\) の最小値は \(\displaystyle\frac{2}{5}\) で
このとき、\(\vec{p},\vec{q}\) の向きが反対あることと、大きさがどちらも1であることから
\(-\vec{p}=\vec{q}\)
③④より
\(\vec{a}=\displaystyle\frac{1}{5}(\vec{p}-2\vec{p})=-\displaystyle\frac{1}{5}\vec{p}\)
\(\vec{b}=\displaystyle\frac{1}{5}(2\vec{p}+\vec{p})=\displaystyle\frac{3}{5}\vec{p}\)
であるから、\(|\vec{a}|=\displaystyle\frac{1}{5}\), \(|\vec{b}|=\displaystyle\frac{3}{5}\)
(注)
\(\vec{p},\vec{q}\)は、\(|\vec{p}|=1\), \(|\vec{q}|=1\) を満たしていれば、
\(\vec{a}=\displaystyle\frac{1}{5}(\vec{p}+2\vec{q})\)・・・③
\(\vec{b}=\displaystyle\frac{1}{5}(2\vec{p}-\vec{q})\)・・・④
に(自由に)\(\vec{p},\vec{q}\)を当てはめて、\(\vec{a},\vec{b}\) を決定すればもとの2つの条件式を満たすので、\(\vec{p},\vec{q}\)は互いに影響せずに独立して動くことができます(始点を原点、終点を円(単位円)上の点として、2つの大きさ1の矢印がグルグル動けるイメージ)。
例題の最大値のときは\(\vec{p},\vec{q}\)が重なるときで、最小値のときは\(\vec{p},\vec{q}\)が反対向きになっているときになります。どの方向に向いているかは任意です。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→内積と等式・不等式の証明 back→内積とベクトルの大きさ①