分数方程式・不等式の解法について見ていきます。
(2)グラフを考えて解く
方法の2パターンになります。
(例題1)
次の不等式を解け。
\(\displaystyle\frac{3x-14}{x-4}≧-2x+11\)
(解法1)式変形で解く
\(x≠4\) で、\((x-4)^2\) を両辺に掛けると
\((3x-14)(x-4)≧(-2x+11)(x-4)^2\)
\(\{3x-14+(2x-11)(x-4)\}(x-4)≧0\)
\(2(x^2-8x+15)(x-4)≧0\)
\((x-3)(x-4)(x-5)≧0\)
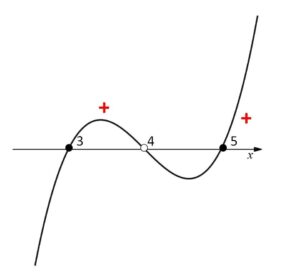
3次関数のグラフを考えると、不等式の解は
\(3≦x<4\), \(x≧5\)
(解答2)分数関数のグラフを考える
\(\displaystyle\frac{3x-14}{x-4}≧-2x+11\) より
\(\displaystyle\frac{3(x-4)-2}{x-4}≧-2x+11\)
\(-\displaystyle\frac{2}{x-4}+3≧-2x+11\)
\(x-4≧\displaystyle\frac{1}{x-4}\)
\(x-4=\displaystyle\frac{1}{x-4}\) を解くと
\((x-4)^2=1\) より \(x=3,5\) (グラフの交点の\(x\)座標)
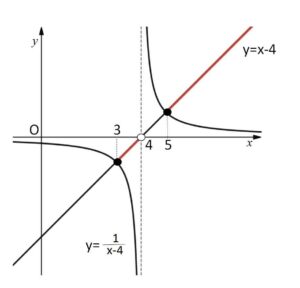
グラフより不等式を満たす範囲は
\(3≦x<4\), \(x≧5\)
(例題2)
方程式
\(\displaystyle\frac{3x-9}{2x+5}=x+k\)
の実数解の個数を調べよ。
(解答)式変形で解く
\(x≠-\displaystyle\frac{5}{2}\) であり、両辺\(2x+5\)倍して
\(3x-9=(2x+5)(x+k)\)・・・①
整理して
\(2x^2+2(k+1)x+5k+9=0\)・・・②
ここで、①に\(x=-\displaystyle\frac{5}{2}\) を代入すると
\(-\displaystyle\frac{33}{2}=0\)
となるから、2次方程式②は\(x=-\displaystyle\frac{5}{2}\)を解に持たない。
よって②において判別式の正負を調べればよく
\(\displaystyle\frac{D}{4}\)
\(=(k+1)^2-2(5k+9)\)
\(=k^2-8k-17\)
であり、\(k^2-8k-17=0\) の解は
\(k=4±\sqrt{33}\) だから
(ア)\(D>0\) つまり
\(k<4-\sqrt{33}\), \(k>4+\sqrt{33}\) のとき
実数解は\(2\)個
(イ)\(D=0\) つまり
\(k=4±\sqrt{33}\) のとき
実数解は\(1\)個
(ウ)\(D<0\) つまり
\(4-\sqrt{33}<k<4+\sqrt{33}\) のとき
実数解は\(0\)個
(参考1)グラフを考えると
\(\displaystyle\frac{3x-9}{2x+5}=x+k\) より
\(\displaystyle\frac{\displaystyle\frac{3}{2}(2x+5)-\displaystyle\frac{15}{2}-9}{2x+5}=x+k\)
\(\displaystyle\frac{-\displaystyle\frac{33}{4}}{x+\displaystyle\frac{5}{2}}+\displaystyle\frac{3}{2}=x+k\)
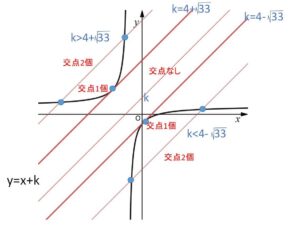
右辺について 直線 \(y=x+k\) は \(k\) を変化させると上下に動く。
左辺について \(y=\displaystyle\frac{-\displaystyle\frac{33}{4}}{x+\displaystyle\frac{5}{2}}+\displaystyle\frac{3}{2}\) は固定された分数関数のグラフ
図示すると次の通りになり、例えば\(k>4+\sqrt{33}\) のときは2つのグラフの交点は\(2\)個になり、実数解の個数も\(2\)個になる。
(参考2)定数分離
\(k\)を分離すると
\(\displaystyle\frac{3x-9}{2x+5}-x=k\)
となりますが、\(y=(左辺)\)のグラフを描くには微分(数Ⅲ)が必要です。ただこの解法もよい方法です。
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→分数方程式・不等式とグラフの共有点② back→分数関数のグラフ