トレミーの定理

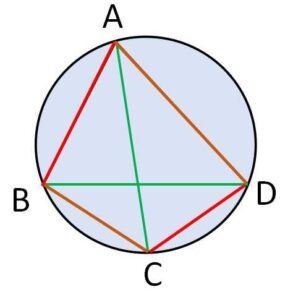
トレミーの定理について見ていきます。

 

・トレミーの定理

(解説)
数式が表すのは「対辺の長さの積の和が対角線の長さの積に等しい」ということです。証明は色々ありますが、手間は掛かりますが覚えやすい(1)余弦定理を用いる方法と、やや技巧的ですが簡潔な(2)補助線を利用した幾何的な方法を紹介します。なお、逆に上記等式が成り立つならば四角形が円に内接することもいえますが(トレミーの定理の逆)、証明は省略します。

(証明1)余弦定理を利用

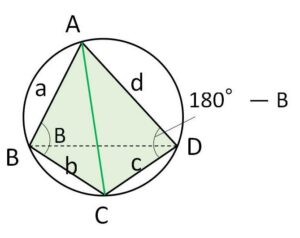
図のように4辺を\(a,b,c,d\)とおいて、対角の和が\(180°\)になることに注意する。
まず\(AC^2\)を2通りに表すと、余弦定理より
\(AC^2=a^2+b^2-2ab\cos B\)・・・①
\(AC^2=c^2+d^2-2cd\cos(180°-B)\) より
\(AC^2=c^2+d^2+2cd\cos B\)・・・②

①×cd+②×ab より\(\cos B\)を消去すると
\((cd+ab)AC^2\)
\(=cd(a^2+b^2)+ab(c^2+d^2)\)
(因数分解すると)
\(=ac(ad+bc)+bd(bc+ad)\)
\(=(ac+bd)(ad+bc)\)
よって
\(AC^2=\displaystyle\frac{(ac+bd)(ad+bc)}{ab+cd}\)・・・③

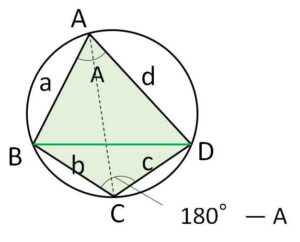
次に\(BD^2\)を2通りに表すと同様に余弦定理より
\(BD^2=a^2+d^2-2ad\cos A\)・・・④
\(BD^2=b^2+c^2+2bc\cos A\)・・・⑤

①×bc+②×ad より\(\cos A\)を消去すると
\((bc+ad)BD^2\)
\(=bc(a^2+d^2)+ad(b^2+c^2)\)
\(=ab(ac+bd)+cd(bd+ac)\)
\(=(ab+cd)(ac+bd)\)
よって
\(BD^2=\displaystyle\frac{(ab+cd)(ac+bd)}{ad+bc}\)・・・⑥

したがって③⑥より
\((AC\cdot BD)^2\)
\(=\displaystyle\frac{(ac+bd)(ad+bc)}{ab+cd}\cdot\displaystyle\frac{(ab+cd)(ac+bd)}{ad+bc}\)
\(=(ac+bd)^2\)

ゆえに
\(AC \cdot BD=ac+db\)
\(AC\cdot BD=AB\cdot CD+AD\cdot BC\)

(③⑥の平方根をとることで対角線の長さを4辺で表すことが可能です。副産物。)

 

(証明2)補助線を引いて相似を利用
補助線を引かずとも既に相似形(方べきの定理で利用したもの)は存在しますが、この状態のままだと証明したい等式の積はでてきません。そこで補助線を引くことになりますが、\(A\)から対角線\(BD\)に「\(\angle CAD=\angle BAE\)」となるように\(AE\)を引きます。

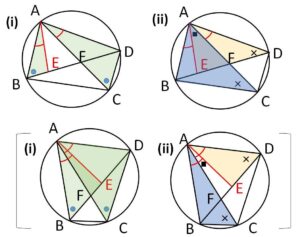
図(i)より
\(△ABE∽△ACD\)だから
\(\displaystyle\frac{AB}{AC}=\displaystyle\frac{BE}{CD}\)
よって
\(AB\cdot CD=AC\cdot BE\)・・・(ア)

また図(ii)より
\(△AED∽△ABC\) だから
\(\displaystyle\frac{AD}{AC}=\displaystyle\frac{ED}{BC}\)
よって
\(AD\cdot BC=AC\cdot ED\)・・・(イ)

(ア)+(イ)より
\(AB\cdot CD+AD\cdot BC\)
\(=AC(BE+ED)\)
\(=AC\cdot BD\)

 

 

(例題)
正三角形\(ABC\)の外接円の\(A\)を含まない弧\(BC\)上に(端点を除く)、点\(P\)をとる。このとき \(AP=BP+CP\) が成り立つことを示せ。

 

(解答)

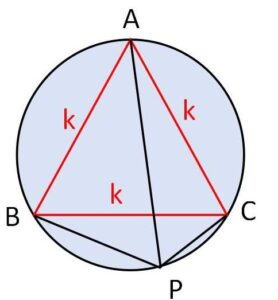
正三角形の一辺の長さを\(k\)とおくと、トレミーの定理より
\(kPC+kBP=kAP\)
よって
\(AP=BP+PC\)

 

 

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→2円の位置関係　back→方べきの定理の逆