空間座標と空間図形

空間図形の問題では、ベクトルや空間座標を用いると解きやすいことが多いです。
今回はそのうち座標を用いて解く例題です。

(例題)
半径\(r\)の球面上に4点\(A,B,C,D\)がある。四面体\(ABCD\)の各辺の長さは、\(AB=\sqrt{3}\)、\(AC=AD=BC=BD=CD=2\) を満たしている。このとき\(r\)の値を求めよ。

(解答)

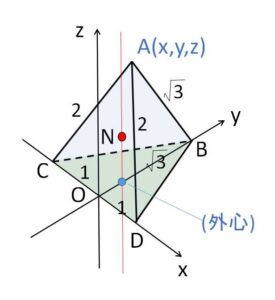
(仲間外れの\(AB\)に着目して、\(B\)を\(y\)軸上にのせています。すると立体の対称性から\(x=0\)が予想できて、計算間違いの確認ができます)

一辺の長さ\(2\)の三角形\(BCD\)の面を、空間座標における\(xy\)平面にのせて
\(C(-1,0,0),\ D(1,0,0),\ B(0,\sqrt{3},0)\)
とする。\(A(x,y,z)\) とおくと条件より

\((x+1)^2+y^2+z^2=4\)・・・①
\((x-1)^2+y^2+z^2=4\)・・・②
\(x^2+(y-\sqrt{3})^2+z^2=3\)・・・③

①－②より
\(x=0\)
これと①－③より
\(y=\displaystyle\frac{\sqrt{3}}{2}\)
さらに①より
\(z=±\displaystyle\frac{3}{2}\)

\(z<0\) の場合は\(xy\)平面について対称な立体ができるだけなので
\(A(0,\displaystyle\frac{\sqrt{3}}{2},\displaystyle\frac{3}{2})\)
だけ考えればよい。

外接球の中心\(N\)は、\(B,C,D\)から等距離にあるので、\(△BCD\)の外心を通り\(z\)軸に平行な直線上にある。\(△BCD\)は正三角形だから \(N(0,\displaystyle\frac{\sqrt{3}}{3},z)\) とおけて、\(NA^2=NB^2\ (=r^2)\) より
\(0^2+(\displaystyle\frac{\sqrt{3}}{3}-\displaystyle\frac{\sqrt{3}}{2})^2+(z-\displaystyle\frac{3}{2})^2=0^2+(\displaystyle\frac{\sqrt{3}}{3}-\sqrt{3})^2+z^2\)
これを解くと \(z=\displaystyle\frac{1}{3}\) だから
\(r=\sqrt{(\displaystyle\frac{\sqrt{3}}{3}-\sqrt{3})^2+(\displaystyle\frac{1}{3})^2}\)

\(=\displaystyle\frac{\sqrt{13}}{3}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→断面の取り出し方　back→立体の面上における最短距離