立体の共通部分 | 教えて数学理科

立体の共通部分に関する例題です。

(例題)
1辺の長さが\(2\)の立方体\(ABCD-EFGH\)がある。
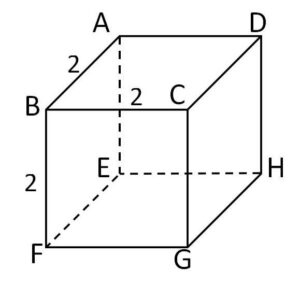
共通部分幾何1
(1)三角柱\(AEF-DHG\)と三角柱\(AEH-BFG\)との共通部分を\(X\)とする。\(X\)の面の数と辺の数を求めよ。また体積と表面積を求めよ。
(2)\(X\)と三角柱\(ABD-EFH\)との共通部分を\(Y\)とする。\(Y\)の面の数と辺の数を求めよ。また体積と表面積を求めよ。

もちろん共通部分をイメージすることも大事ですが、理屈で判断すると次のようになります。
(i)2つの平面の共通部分は交線または平面。これが共通部分の枠組みになる。
(ii)平面上の2点を結んだ直線上の点はこの平面上にある。よって2平面のいずれもが通る2点を発見できればそれを結べば交線になる。

(解答)
(1)

三角柱は全部で5面あるので、\(5×5=25\) 通りの共通部分を調べるの面倒です。そこで4面は立方体の面上にあることから、立方体の6面上の共通部分と、内部にある1面同士の共通部分を調べます。

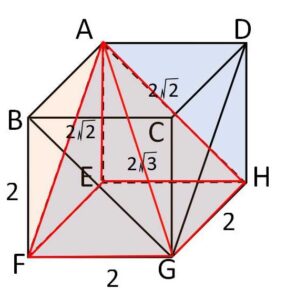
共通部分幾何2
2つの三角柱の立方体の面上での共通部分は
\(△AEF,△AEH,\)正方形\(EFGH\)
立方体の内部については、面\(AFGD\)と面\(AHGB\)の共通部分の\(AG\)。
よって立体\(X\)は四角錐\(A-EFGH\)となる。

\(X\)の面の数は\(5\)、辺の数は\(8\)。
体積\(V_1\)は
\(V_1=\displaystyle\frac{1}{3}\cdot2^2\cdot2=\)\(\displaystyle\frac{8}{3}\)
表面積\(S_1\)は
\(S_1=2△AEF+2△AFG+正方形EFGH\)
\(=2\cdot\displaystyle\frac{1}{2}\cdot2^2+2\cdot\displaystyle\frac{1}{2}\cdot2\cdot2\sqrt{2}+2^2\)　(\(\angle AFG=90°\) より)
\(=8+4\sqrt{2}\)

(2)

3つ目の三角柱も立方体のちょうど半分で、\(Y\)は\(X\)を立方体を半分にする面\(BFHD\)で切断してできた立体と考えると分かりやすいです。もちろん(1)のように吟味してもよいです。

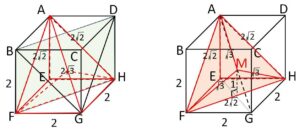
共通部分幾何3

\(Y\)は(1)の\(X\)を面\(BFHD\)で切断してできた立体のうち\(A\)を含むものである。
面\(BFHD\)の切断面は、\(M\)を立方体の対角線の中点とすれば\(△MFH\)であり、\(Y\)は右上図のような立体である。
よって\(Y\)の面の数は\(6\)、辺の数は\(9\)。
体積\(V_2\)は、\(X\)から三角錐\(M-FGH\)を除くことにより
\(V_2=\displaystyle\frac{8}{3}-\displaystyle\frac{1}{3}\cdot\displaystyle\frac{1}{2}\cdot2^2\cdot1=\)\(2\)
表面積\(S_2\)は
\(S_2=3△AFE+3△MFH\)
\(=3(\displaystyle\frac{1}{2}\cdot2^2+\displaystyle\frac{1}{2}\cdot2\sqrt{2}\cdot1)\)
\(=6+3\sqrt{2}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→立体ができる条件　 back→断面の取り出し方