正多面体どうしの位置関係について見ていきます。
・正四面体と立方体
立方体の8頂点うち隣り合わない4頂点を選んで結んで立体を作ると、どの辺も正方形の対角線になることから正四面体になります。このように正四面体を立方体に埋め込むと立体的な配置が分かりやすくなります。図では1つの正四面体を図示していますが、白丸の点を結ぶともう1つの正四面体ができます。
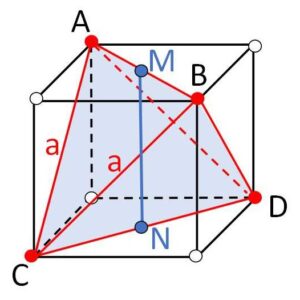
正方形の対角線は垂直に交わるので
\(AB \perp CD\)
また、\(AB,CD\)の中点を\(M,N\)とすると、\(MN\)は立方体の高さになります。よって
\(MN \perp AB\)、\(MN \perp CD\)
正四面体の一辺の長さを\(a\)とすれば、立方体の一辺の長さは\(\displaystyle\frac{a}{\sqrt{2}}\)なので
\(MN=\displaystyle\frac{a}{\sqrt{2}}\)
他にも正四面体の体積を立方体から削って求めることなどもできます。
・正八面体と立方体・正四面体
正八面体も立方体に埋め込むことができます。
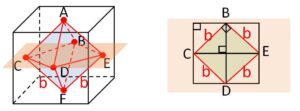
立方体の6面の中心(対角線の交点)を結ぶと各線分の長さは全て等しくなるので、正八面体ができます。\(B,C,D,E\)は同じ平面上にあり、この平面は上面と平面に平行でちょうど真ん中を通っています。上右図より四角形\(BCDE\)は正方形であることが分かり、正八面体の一辺の長さを\(b\)とすると、立方体の一辺の長さは
\(\displaystyle\frac{b}{\sqrt{2}}\cdot2=\)\(\sqrt{2}b\)
です。これらのことを利用すると正八面体の体積\(V\)を、2つの正四角錐の和として求めることができます。
\(V=\displaystyle\frac{1}{3}b^2\cdot\sqrt{2}b=\displaystyle\frac{\sqrt{2}}{3}b^3\)
なお、正方形は他にも四角形\(ADFB,ACFE\)の2つが存在します。
続いて、正四面体と正八面体の位置関係について考えてみます。
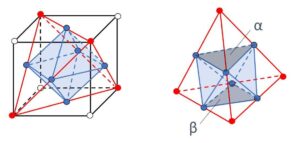
左図の正四面体の辺の中点は、立方体の面である正方形の中心になるので、これらの中点を正四面体の面である正三角形の1辺の長さの半分になるように結ぶと、正八面体ができます。すると、右図のように正四面体の1面を床に置くと、正八面体の向かい合う面\(α,β\)が平行であることが分かります。また、右図より正八面体の体積を正四面体から削り出すことによって求めることもできます。
ところで、左図の白丸を結ぶともう1つの正四面体ができますが、この正四面体の辺の中点は同じ正八面体の頂点になります。よって2つの正四面体の共通部分は正八面体であることが予想できますが、これは正しいです。2つの正四面体の面の交線を考えることにすると、4×4=16 通りの組み合わせがありますが、このうち12通りが交わり(4通りは交線をもたない)、12本の線分により正八面体ができます。もしくは、一方の正四面体をもう一方の正四面体の4つの面で切断することで、4つの正三角形の面が増えるので、4+4=8 面の正八面体ができると考えてもよいです。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→等面四面体 back→オイラーの多面体定理