球面と球面

球面と球面の交わりに関する例題です。

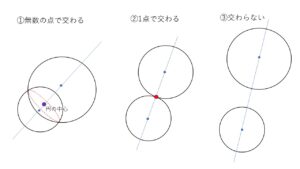
球面と球面の位置関係は次の3パターンに分類されます。
①無数の点で交わる(交線は円になる)　②1点で交わる(接する)　③交わらない(共有点なし)
①において交線が円になるのは、2つの球の中心を通る平面による切断面を考えると分かります。もしくは、2つの球の方程式から交線が1つの平面上にある(例題1 参照)ことと、平面と球の交線が円になることからも分かります。

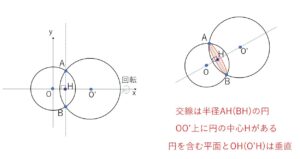
(例題1)
2つの球面
\((x-1)^2+(y-1)^2+(z-1)^2=7\)
\((x-2)^2+(y-3)^2+(z-3)^2=1\)
が交わってできる円を含む平面の方程式を求めよ。

(解答)
2つの球面
\(S_1:(x-1)^2+(y-1)^2+(z-1)^2-7=0\)
\(S_2:(x-2)^2+(y-3)^2+(z-3)^2-1=0\)
について

方程式
\((x-1)^2+(y-1)^2+(z-1)^2-7+k\{(x-2)^2+(y-3)^2+(z-3)^2-1\}=0\)

は、2つの球面の交線を通る図形の方程式を表す。\(k≠-1\)のときは球面になり、\(k=-1\)のときは平面になるので、求める平面の方程式は

\((x-1)^2+(y-1)^2+(z-1)^2-7-\{(x-2)^2+(y-3)^2+(z-3)^2-1\}=0\)

整理すると
\(2x+4y+4z-25=0\)

(例題2)
座標空間内の2つの球面
\(S_1:(x-1)^2+(y-1)^2+(z-1)^2=7\)
\(S_2:(x-2)^2+(y-3)^2+(z-3)^2=1\)
を考える。\(S_1\)と\(S_2\)の共通部分を\(C\)とする。このとき以下の問いに答えよ。

(1)\(S_1\)との共通部分が\(C\)となるような球面のうち、半径が最小となる球面の方程式を求めよ。
(2)\(S_1\)との共通部分が\(C\)となるような球面のうち、半径が\(\sqrt{3}\)となる球面の方程式を求めよ。

(解答)
(1)
\(S_1:(x-1)^2+(y-1)^2+(z-1)^2=7\)・・・①
中心 \(O_1(1,1,1)\) 半径\(\sqrt{7}\)

\(S_2:(x-2)^2+(y-3)^2+(z-3)^2=1\)・・・②
中心 \(O_2(2,3,3)\) 半径\(1\)

\(O_1O_2=\sqrt{1^2+2^2+2^2}=3\)
\(\sqrt{7}-1<3<\sqrt{7}+1\)
より、\(S_1,S_2\)の共通部分は円\(C\)になる。

円\(C\)を含む平面\(α\)の方程式は①－②より
\(2x+4y+4z-25=0\)・・・③

また、\(O_1\)から平面\(α\)に下ろした垂線の足\(H\)は円\(C\)の中心である。
同様に\(O_2\)から平面\(α\)に下ろした垂線の足も円\(C\)の中心だから、\(O_1,H,O_2\)は一直線上にある。

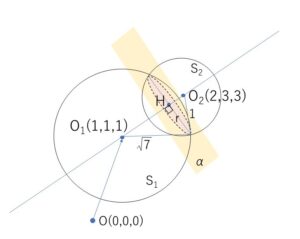
\(\overrightarrow{OH}=\overrightarrow{OO_1}+k\overrightarrow{O_1O_2}\)
\(=(1,1,1)+k(1,2,2)\)
\(=(1+k,1+2k,1+2k)\)・・・④

④を \(α:2x+4y+4z-25=0\)・・・③ に代入して
\(2(1+k)+4(1+2k)+4(1+2k)-25=0\)
\(k=\displaystyle\frac{5}{6}\)

よって④より
\(H(\displaystyle\frac{11}{6},\displaystyle\frac{8}{3},\displaystyle\frac{8}{3})\)

そして円\(C\)の半径を\(r\)とすると
\(O_1H=\sqrt{(\displaystyle\frac{5}{6})^2+(\displaystyle\frac{5}{3})^2+(\displaystyle\frac{5}{3})^2}=\displaystyle\frac{5}{2}\)　より

\(r=\sqrt{7-(\displaystyle\frac{5}{2})^2}\)\(=\displaystyle\frac{\sqrt{3}}{2}\)

ここで、求める球面\(K\)の大円が円\(C\)となるときが球面の半径が最小となるときであるから、
球面\(K\)の中心が\(H(\displaystyle\frac{11}{6},\displaystyle\frac{8}{3},\displaystyle\frac{8}{3})\)、半径が\(\displaystyle\frac{\sqrt{3}}{2}\) となるので、球面\(K\)の方程式は

\((x-\displaystyle\frac{11}{6})^2+(y-\displaystyle\frac{8}{3})^2+(z-\displaystyle\frac{8}{3})^2=\displaystyle\frac{3}{4}\)

(2)

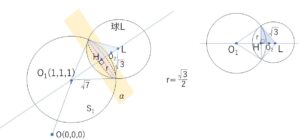
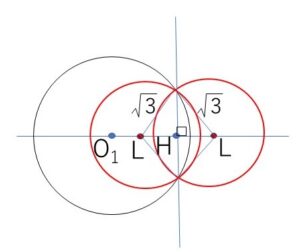
求める球面を球面\(L\)とし、その中心を\(L\)とする。
\(LH^2=3-(\displaystyle\frac{\sqrt{3}}{2})^2=\displaystyle\frac{9}{4}\)・・・⑤

\(L\)は\(O_1O_2\)上にあるので、(1)より
\(\overrightarrow{OL}=(1+k,1+2k,1+2k)\)・・・⑥

となり、\(H(\displaystyle\frac{11}{6},\displaystyle\frac{8}{3},\displaystyle\frac{8}{3})\) より

\(LH^2=(k-\displaystyle\frac{5}{6})^2+(2k-\displaystyle\frac{5}{3})^2+(2k-\displaystyle\frac{5}{3})^2\)・・・⑦

⑤⑦より
\(9k^2-\displaystyle\frac{45}{3}k+\displaystyle\frac{225}{36}=\displaystyle\frac{9}{4}\)

\(9k^2-15k+4=0\)
\((3k-4)(3k-1)=0\)
\(k=\displaystyle\frac{4}{3},\displaystyle\frac{1}{3}\)

よって⑥より球面\(L\)の中心の座標は
\((\displaystyle\frac{7}{3},\displaystyle\frac{11}{3},\displaystyle\frac{11}{3})\) または \((\displaystyle\frac{4}{3},\displaystyle\frac{5}{3},\displaystyle\frac{5}{3})\)

したがって方程式は
\((x-\displaystyle\frac{7}{3})^2+(y-\displaystyle\frac{11}{3})^2+(z-\displaystyle\frac{11}{3})^2=3\)
または
\((x-\displaystyle\frac{4}{3})^2+(y-\displaystyle\frac{5}{3})^2+(z-\displaystyle\frac{5}{3})^2=3\)

条件に合う球面は2つあります。2つの球面の中心は\(H\)の両側にそれぞれありますが、次の断面図を参考にしてください。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→空間図形の証明問題　back→球面と平面