空間ベクトルの終点の存在範囲

\(\overrightarrow{OP}=r\overrightarrow{OA}+s\overrightarrow{OB}+t\overrightarrow{OC}\) によって定まる\(P\)の動く領域について見ていきます。

まずは、\(P\)が平面\(ABC\)上にある条件をおさらいしておきます。

・四面体の内部にある条件
四面体\(OABC\)において

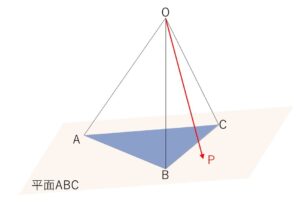
空間ベクトル終点1

\(\overrightarrow{OP}=r\overrightarrow{OA}+s\overrightarrow{OB}+t\overrightarrow{OC}\)・・・①

を満たすように\(P\)が動くとします。

(i)\(r+s+t=1\) のとき
\(P\)は平面\(ABC\)上を

(ii)\(r+s+t=1\),　\(r≧0\), \(s≧0\), \(t≧0\) のとき
\(P\)は三角形\(ABC\)の周および内部を

それぞれ動きます。(詳しくは →(3-5)同一平面上にある条件① を参照してください)

次に
\(0≦r+s+t≦1\),　\(r≧0\), \(s≧0\), \(t≧0\) のとき
\(P\)が動く領域を考えます。

和の部分が動くので、\(r+s+t=k\) と固定します。この等式の両辺を\(k\)で割ることで、(係数の和)=1 の形に帰着させます。

(ア)\(r+s+t=0\) のとき
\(r,s,t\)はすべて\(0\)以上の値だから、\(r=s=t=0\)
よって
\(\overrightarrow{OP}=r\overrightarrow{OA}+s\overrightarrow{OB}+t\overrightarrow{OC}=\vec{0}\)
より、\(P\)は\(O\)と一致する。

(イ)\(0<r+s+t≦1\) のとき
\(r+s+t=k\) とおくと、\(0<k≦1\)

等式の両辺を\(k\)で割ると
\(\displaystyle\frac{r}{k}+\displaystyle\frac{s}{k}+\displaystyle\frac{t}{k}=1\)・・・②

また、\(r,s,t≧0\),　\(k>0\) より
\(\displaystyle\frac{r}{k}≧0\),　\(\displaystyle\frac{s}{k}≧0\),　\(\displaystyle\frac{t}{k}≧0\)・・・③

\(\overrightarrow{OP}=r\overrightarrow{OA}+s\overrightarrow{OB}+t\overrightarrow{OC}\)

\(=\displaystyle\frac{r}{k}(k\overrightarrow{OA})+\displaystyle\frac{s}{k}(k\overrightarrow{OB})+\displaystyle\frac{t}{k}(k\overrightarrow{OC})\)

(係数の和)=1 の形に変形できたので、あとは \(k\overrightarrow{OA},k\overrightarrow{OB},k\overrightarrow{OC}\) がどの位置にあるかを検討します。

ここで、
\(k\overrightarrow{OA}=\overrightarrow{OA’}\),　\(k\overrightarrow{OB}=\overrightarrow{OB’}\),　\(k\overrightarrow{OC}=\overrightarrow{OC’}\)
とおくと、\(0<k≦1\) より、\(A’,B’,C’\)はそれぞれ辺\(OA,OB,OC\)上(ただし\(O\)は除く)にある。(このとき\(△ABC\)と\(△A’B’C’\)は相似になる)

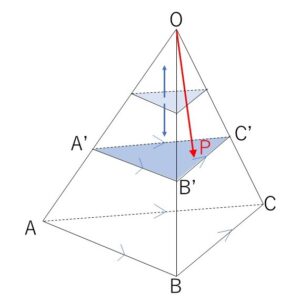
空間ベクトル終点2

\(k\)を固定すると
\(\overrightarrow{OP}=\displaystyle\frac{r}{k}\overrightarrow{OA’}+\displaystyle\frac{s}{k}\overrightarrow{OB’}+\displaystyle\frac{t}{k}\overrightarrow{OC’}\)
と②③より、\(P\)は\(△A’B’C’\)の周および内部を動き、\(△A’B’C’\)は平面\(ABC\)に平行だから、\(k\)を \(0<k≦1\) の範囲で動かすことで四面体\(OABC\)の表面および内部(ただし\(O\)を除く)を動く。

以上(ア)(イ)より
\(0≦r+s+t≦1\),　\(r≧0\), \(s≧0\), \(t≧0\) のとき
\(P\)は四面体\(OABC\)の表面および内部を動く。

\(0≦r+s+t\) の部分はあってもなくてもよいです(\(r,s,t≧0\)で保証されるので)。
それと、ざっくりとしたイメージですが、「和」の式は四面体の切り口の三角形の大きさを決定して、「係数の符号や大小」は切り口での動く範囲を決定します。次の例題の解答の目安にしてください。

(例題)
四面体\(OABC\)がある。\(r,s,t\)を実数とし、点\(P\)を次の等式で定める。
\(\overrightarrow{OP}=r\overrightarrow{OA}+s\overrightarrow{OB}+t\overrightarrow{OC}\)
\(r,s,t\)が次の各条件を満たすとき、点\(P\)の存在範囲を求めよ。

(1)\(r+2s+3t=1\)
(2)\(r+s+t≦3\),　\(r≧0\), \(s≧0\), \(t≧0\)
(3)\(r+s+t=1\),　\(r≧s≧t≧0\)
(4)\(r+s+t≦3\),　\(r≧s≧t≧0\)

(解答)
(1)

\(r\overrightarrow{OA}+s\overrightarrow{OB}+t\overrightarrow{OC}\) の係数の和が\(1\)になるように変形します。

\(\overrightarrow{OP}=r\overrightarrow{OA}+s\overrightarrow{OB}+t\overrightarrow{OC}\)

\(=r\overrightarrow{OA}+2s(\displaystyle\frac{1}{2}\overrightarrow{OB})+3t(\displaystyle\frac{1}{3}\overrightarrow{OC})\)

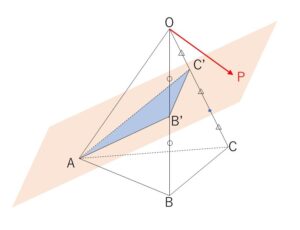
\(\displaystyle\frac{1}{2}\overrightarrow{OB}=\overrightarrow{OB’}\),　\(\displaystyle\frac{1}{3}\overrightarrow{OC}=\overrightarrow{OC’}\) とおくと

\(\overrightarrow{OP}=r\overrightarrow{OA}+2s\overrightarrow{OB’}+3t\overrightarrow{OC’}\)

\(r+2s+3t=1\) より、\(P\)は平面\(AB’C’\)上を動く。

空間ベクトル終点例題1-1

(2)

\(r+s+t=k\) とおいて固定すると、三角形の周および内部になり、\(k\)を動かすことで四面体を作り出します。

\(r+s+t≦3\),　\(r≧0\), \(s≧0\), \(t≧0\)

(ア)\(r+s+t=0\) のとき
\(r,s,t≧0\) より \(r=s=t=0\)
よって \(\overrightarrow{OP}=\vec{0}\) となるから、\(P\)は\(O\)と一致する。

(イ)\(0<r+s+t≦3\) のとき
\(r+s+t=k\) とおくと、\(0<k≦3\)
等式の両辺を\(k\)で割ると
\(\displaystyle\frac{r}{k}+\displaystyle\frac{s}{k}+\displaystyle\frac{t}{k}=1\)・・・①

また、\(r,s,t≧0\),　\(k>0\) より
\(\displaystyle\frac{r}{k}≧0\), \(\displaystyle\frac{s}{k}≧0\), \(\displaystyle\frac{t}{k}≧0\)・・・②

\(\overrightarrow{OP}=r\overrightarrow{OA}+s\overrightarrow{OB}+t\overrightarrow{OC}\)

\(=\displaystyle\frac{r}{k}(k\overrightarrow{OA})+\displaystyle\frac{s}{k}(k\overrightarrow{OB})+\displaystyle\frac{t}{k}(k\overrightarrow{OC})\)

\(k\)はMaxで\(3\)までとるので、\(OA,OB,OC\)を3倍に延長した先の点を考えます。

\(k\overrightarrow{OA}=\overrightarrow{OA’}\),　\(k\overrightarrow{OB}=\overrightarrow{OB’}\),　\(k\overrightarrow{OC}=\overrightarrow{OC’}\) とおいて、
\(3\overrightarrow{OA}=\overrightarrow{OX}\),　\(3\overrightarrow{OB}=\overrightarrow{OY}\),　\(3\overrightarrow{OC}=\overrightarrow{OZ}\) を満たすように\(X,Y,Z\)を定める。すると、\(A’,B’,C’\)は線分\(OX,OY,OZ\)上(\(O\)を除く)を動く。

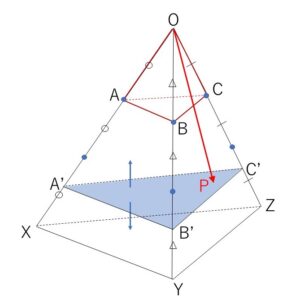
空間ベクトル終点例題1-2

\(\overrightarrow{OP}=\displaystyle\frac{r}{k}\overrightarrow{OA’}+\displaystyle\frac{s}{k}\overrightarrow{OB’}+\displaystyle\frac{t}{k}\overrightarrow{OC’}\)

と①②より、\(k\)を固定すると\(P\)は\(△A’B’C’\)の周および内部を動き、\(0<k≦3\) の範囲で\(k\)を動かすことにより、\(P\)は四面体\(OXYZ\)の表面および内部を動く(\(O\)は除く)。

以上(ア)(イ)より
\(P\)は四面体\(OXYZ\)の表面および内部を動く。

(3)

\(r+s+t=1\),　\(r,s,t≧0\) だと\(△ABC\)の周および内部を動きますが、
\(r≧s≧t\) (\(≧0\)) の大小制限により、\(△ABC\)の一部分を動くことになります。
典型的なパターン例ではないので、\(r+s+t=1\) から1文字消去して、
\(\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}\)
(\(\overrightarrow{OP}=\overrightarrow{OA}+s\overrightarrow{AB}+t\overrightarrow{AC}\) でもよい)
の形に戻してどの部分を動くか調べていきます。

\(r+s+t=1\),　\(r≧s≧t≧0\)

\(r=1-s-t\) より

\(\overrightarrow{OP}=r\overrightarrow{OA}+s\overrightarrow{OB}+t\overrightarrow{OC}\)

\(=(1-s-t)\overrightarrow{OA}+s\overrightarrow{OB}+t\overrightarrow{OC}\)

\(=\overrightarrow{OA}+s(\overrightarrow{OB}-\overrightarrow{OA})+t(\overrightarrow{OC}-\overrightarrow{OA})\)

\(=\overrightarrow{OA}+s\overrightarrow{AB}+t\overrightarrow{AC}\)

よって
\(\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}\)

また不等式 \(r≧s≧t≧0\) は
\(1-s-t≧s≧t≧0\) となるから

\(2s+t≦1\) かつ \(s≧t≧0\)

\(2s+t≦1\), \(s≧0\), \(t≧0\) の部分は三角形の周および内部に帰着できるとして、問題は \(s≧t\) の部分です。しかしこれも \(\overrightarrow{AB},\overrightarrow{AC}\) 方向を、直交座標と対応させることで解決できます。

ここで
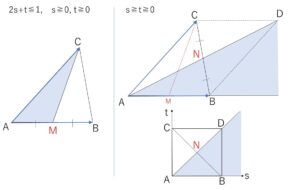
\(2s+t≦1\),　\(s≧0\),　\(t≧0\) のとき
\(\overrightarrow{AP}=2s(\displaystyle\frac{1}{2}\overrightarrow{AB})+t\overrightarrow{AC}\)
より、\(AB\)の中点を\(M\)とすると、\(P\)は\(△AMC\)の周および内部を動き、

\(s≧t≧0\) のとき
\(\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}\)
より、\(BC\)の中点を\(N\)とすると、図のように半直線\(AB,AN\)で挟まれた部分を\(P\)は動く。

空間ベクトル終点例題1-3

よって共通部分を考えると
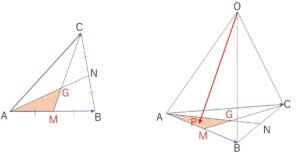
\(2s+t≦1\) かつ \(s≧t≧0\) のとき
\(CM\)と\(AN\)の交点を\(G\)とすると、中線の交点だから\(G\)は\(△ABC\)の重心であり、
\(P\)は、\(△AMG\)の周および内部を動く。

空間ベクトル終点例題2-4

(4)

(2)と同様に\(r+s+t=k\) とおいて、\(k\)を固定させて考えます。また、(3)の拡張的な問題でもあるので途中から(3)と同様に進めていきます。
なお \(k=1\)のときが(3)に対応します。

\(r+s+t≦3\),　\(r≧s≧t≧0\)

(ア)\(r+s+t=0\) のとき
\(r≧s≧t≧0\) より \(r=s=t=0\)
\(\overrightarrow{OP}=\vec{0}\) となるから
\(P\)は\(O\)と一致する。

(イ)\(0<r+s+t≦3\) のとき
\(r+s+t=k\) とおくと、\(0<k≦3\)

等式の両辺を\(k\)で割ると
\(\displaystyle\frac{r}{k}+\displaystyle\frac{s}{k}+\displaystyle\frac{t}{k}=1\)・・・③

また、\(r≧s≧t≧0\),　\(k>0\) より
\(\displaystyle\frac{r}{k}≧\displaystyle\frac{s}{k}≧\displaystyle\frac{t}{k}≧0\)・・・④

\(\overrightarrow{OP}=r\overrightarrow{OA}+s\overrightarrow{OB}+t\overrightarrow{OC}\)

\(=\displaystyle\frac{r}{k}(k\overrightarrow{OA})+\displaystyle\frac{s}{k}(k\overrightarrow{OB})+\displaystyle\frac{t}{k}(k\overrightarrow{OC})\)　(係数の和が1)

\(k\overrightarrow{OA}=\overrightarrow{OA’}\),　\(k\overrightarrow{OB}=\overrightarrow{OB’}\),　\(k\overrightarrow{OC}=\overrightarrow{OC’}\) とおくと

\(\overrightarrow{OP}=\displaystyle\frac{r}{k}\overrightarrow{OA’}+\displaystyle\frac{s}{k}\overrightarrow{OB’}+\displaystyle\frac{t}{k}\overrightarrow{OC’}\)

③より\(r\)を消去すると
\(\overrightarrow{OP}=\displaystyle\frac{r}{k}\overrightarrow{OA’}+\displaystyle\frac{s}{k}\overrightarrow{OB’}+\displaystyle\frac{t}{k}\overrightarrow{OC’}\)

\(=(1-\displaystyle\frac{s}{k}-\displaystyle\frac{t}{k})\overrightarrow{OA’}+\displaystyle\frac{s}{k}\overrightarrow{OB’}+\displaystyle\frac{t}{k}\overrightarrow{OC’}\)

\(=\overrightarrow{OA’}+\displaystyle\frac{s}{k}\overrightarrow{A’B’}+\displaystyle\frac{t}{k}\overrightarrow{A’C’}\)

\(\displaystyle\frac{s}{k}=s’\),　\(\displaystyle\frac{t}{k}=t’\) と置きなおすと

\(\overrightarrow{A’P}=s\overrightarrow{A’B’}+t\overrightarrow{A’C’}\)・・・⑤

(⑤より\(P\)は平面\(A’B’C’\)上にあり、この平面は平面\(ABC\)に平行)

また不等式④は
\(1-s’-t’≧s’≧t’≧0\) となるから
\(2s’+t’≦1\) かつ \(s’≧t’≧0\)・・・⑥

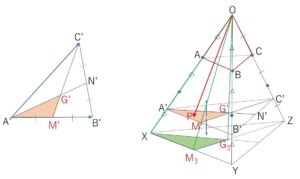
よって(3)と同様に考えると、\(k\)を固定したとき⑤⑥から決定される\(P\)は、\(A’B’\)の中点を\(M’\)、\(△A’B’C’\)の重心を\(G’\)とすれば、\(△A’M’G’\)の周および内部を動く。

空間ベクトル終点例題2-5

ここで、\(0<k≦3\) で
\(\overrightarrow{OA’}=k\overrightarrow{OA}\)

\(\overrightarrow{OM’}=\displaystyle\frac{1}{2}(\overrightarrow{OA’}+\overrightarrow{OB’})\)\(=\displaystyle\frac{1}{2}k(\overrightarrow{OA}+\overrightarrow{OB})\)

\(\overrightarrow{OG’}=\displaystyle\frac{1}{3}(\overrightarrow{OA’}+\overrightarrow{OB’}+\overrightarrow{OC’})\)\(=\displaystyle\frac{1}{3}k(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})\)

だから、\(\overrightarrow{OX}=3\overrightarrow{OA}\),　\(\overrightarrow{OY}=3\overrightarrow{OB}\),　\(\overrightarrow{OZ}=3\overrightarrow{OC}\) とし、
\(XY\)の中点を\(M_3\)、\(△XYZ\)の重心を\(G_3\)とおくと

\(A’,M’,G’\)はそれぞれ線分\(OX,OM_3,OG_3\) 上を動く。(\(O\)は除く)

したがって、\(k\)を動かすことにより\(P\)は四面体\(OXM_3G_3\)の表面および内部を動く。(\(O\)は除く)

以上(ア)(イ)より
\(P\)は四面体\(OXM_3G_3\)の表面および内部を動く。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→正射影と空間図形の方程式　 back→空間ベクトルによる軌跡・領域(投影)