平面に下ろした垂線に関する例題について見ていきます。
(例題1)
\(A(2,0,-3)\), \(B(0,2,-1)\), \(C(8,0,1)\) を通る平面\(π\)に関する \(P(1,-3,4)\) の対称点\(Q\)の座標と\(PQ\)の長さを求めよ。
\(PH\)が\(\overrightarrow{AB},\overrightarrow{AC}\)に垂直であることを利用していきますが、
(1)\(\overrightarrow{AH}=s\overrightarrow{AB}+t\overrightarrow{AC}\) として、\(s,t\)を決定する方法
(2)平面の法線ベクトル、平面の方程式を求める方法
の2パターンでやりたいと思います。
(解法1)
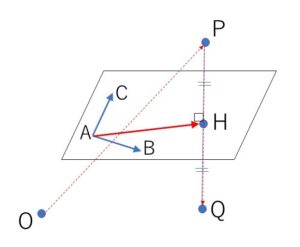
\(PQ\)と平面\(π\)の交点を\(H\)とする。
\(H\)は平面\(π\)上にあるので、実数\(s,t\)を用いると
\(\overrightarrow{AH}=s\overrightarrow{AB}+t\overrightarrow{AC}\)
よって
\(\overrightarrow{PH}=\overrightarrow{AH}-\overrightarrow{AP}\)
\(=s\overrightarrow{AB}+t\overrightarrow{AC}-\overrightarrow{AP}\)・・・①
\(PH\)は平面\(π\)に垂直なので
\(\overrightarrow{AB}\cdot\overrightarrow{PH}=0\)
\(\overrightarrow{AC}\cdot\overrightarrow{PH}=0\)
よって
\(\overrightarrow{AB}\cdot(s\overrightarrow{AB}+t\overrightarrow{AC}-\overrightarrow{AP})=0\)・・・②
\(\overrightarrow{AC}\cdot(s\overrightarrow{AB}+t\overrightarrow{AC}-\overrightarrow{AP})=0\)・・・③
\(A(2,0,-3)\), \(B(0,2,-1)\), \(C(8,0,1)\), \(P(1,-3,4)\) より
\(\overrightarrow{AB}=(-2,2,2)\), \(\overrightarrow{AC}=(6,0,4)\), \(\overrightarrow{AP}=(-1,-3,7)\) となるから
\(|\overrightarrow{AB}|^2=12\), \(|\overrightarrow{AC}|^2=52\),
\(\overrightarrow{AB}\cdot\overrightarrow{AC}=-4\), \(\overrightarrow{AB}\cdot\overrightarrow{AP}=10\), \(\overrightarrow{AC}\cdot\overrightarrow{AP}=22\)
②③より
\(12s-4t-10=0\)
\(-4s+52t-22=0\)
よって \(s=1\), \(t=\displaystyle\frac{1}{2}\)
したがって①より
\(\overrightarrow{PH}=(-2,2,2)+\displaystyle\frac{1}{2}(6,0,4)-(-1,-3,7)\)
\(=(2,5,-3)\)
ゆえに
\(\overrightarrow{OQ}=\overrightarrow{OP}+2\overrightarrow{PH}\)
\(=(1,-3,4)+2(2,5,-3)\)
\(=(5,7,-2)\)
\(Q\)の座標は \((5,7,-2)\)
また
\(|\overrightarrow{PQ}|=|2\overrightarrow{PH}|\)
\(=|(4,10,-6)|\)
\(=2\sqrt{38}\)
(解法2)
\(A(2,0,-3)\), \(B(0,2,-1)\), \(C(8,0,1)\) \(P(1,-3,4)\)
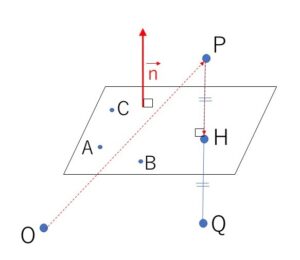
\(\overrightarrow{AB}=(-2,2,2)\), \(\overrightarrow{AC}=(6,0,4)\) に垂直なベクトルを \(\vec{n}=(a,b,c)\) とおくと
\(-2a+2b+2c=0\)・・・(i)
\(6a+4c=0\)・・・(ii)
(ii)より \(c=-\displaystyle\frac{3}{2}a\)
(i)より \(b=a-c=\displaystyle\frac{5}{2}a\)
よって \(\vec{n}=(a,\displaystyle\frac{5}{2}a,-\displaystyle\frac{3}{2}a)\) より \(a=2\) として平面\(π\)に垂直なベクトルの1つは \((2,5,-3)\) となる。平面\(π\)は\(A\)を通るからその方程式は
\(2(x-2)+5y-3(z+3)=0\)
整理して
\(2x+5y-3z=13\)・・・(iii)
\(PQ\)と平面\(π\)の交点を\(H\)とすると、\(PH\)と平面\(π\)が垂直であるから
\(\overrightarrow{PH}=k(2,5,-3)\) と表せるので
\(\overrightarrow{OH}=\overrightarrow{OP}+\overrightarrow{PH}\)
\(=(1,-3,4)+k(2,5,-3)\)
\(=(1+2k,-3+5k,4-3k)\)
\(H\)は平面\(π\)上にあるので(iii)より
\(2(1+2k)+5(-3+5k)-3(4-3k)=13\)
\(k=1\)
したがって、\(\overrightarrow{PH}=(2,5,-3)\) となるので
\(\overrightarrow{OQ}=\overrightarrow{OP}+2\overrightarrow{PH}\)
\(=(1-3,4)+2(2,5,-3)\)
\(=(5,7,-2)\)
\(Q\)の座標は \((5,7,-2)\)
また
\(|\overrightarrow{PQ}|=|2\overrightarrow{PH}|\)
\(=|(4,10,-6)|\)
\(=2\sqrt{38}\)
(例題2)
座標空間において、3点 \(A(\displaystyle\frac{1}{a},0,0)\), \(B(0,\displaystyle\frac{1}{b},0)\), \(C(0,0,\displaystyle\frac{1}{c})\) を通る平面を\(α\)とする。ただし、\(a,b,c\)は正の数とする。平面\(α\)に垂直で原点\(O\)を通る直線と、\(α\)との交点を\(H\)とおく。次の問いに答えよ。
(1)点\(H\)の座標と線分\(OH\)の長さを\(a,b,c\)を用いて表せ。
(2)\(c=\displaystyle\frac{1}{\sqrt{3}}\)とする。2点\(A,B\)が条件 \(OH=1\) を満たしながら動くとき、\(△ABC\)の面積\(S\)の最小値を求めよ。
(解答)
(1)
例題1の1つめの解答のように、\(\overrightarrow{AH}=s\overrightarrow{AB}+t\overrightarrow{AC}\) とおいて、\(s,t\)を決定してもよいです。
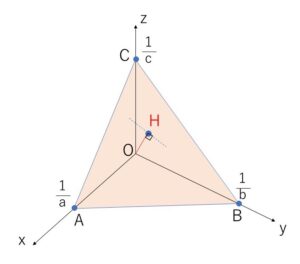
\(A(\displaystyle\frac{1}{a},0,0)\), \(B(0,\displaystyle\frac{1}{b},0)\), \(C(0,0,\displaystyle\frac{1}{c})\) を通る平面\(α\)の方程式を
\(px+qy+rz+s=0\)・・・① とおくと
\(\displaystyle\frac{p}{a}+s=0\), \(\displaystyle\frac{q}{b}+s=0\), \(\displaystyle\frac{r}{c}+s=0\)
\(p=-sa\), \(q=-sb\), \(r=-sc\) を①に代入して
\(-sax-sby-scz+s=0\)
\(s=0\)とすると平面を表さないので、\(s≠0\)。
よって平面\(α\)の方程式は
\(ax+by+cz-1=0\)・・・②
平面\(α\)の法線ベクトルの1つは②より \((a,b,c)\) だから
\(\overrightarrow{OH}=k(a,b,c)\) とおける。
\(H(ka,kb,kc)\)は平面\(α\)上の点だから②に代入して
\(ka^2+kb^2+kc^2-1=0\)
したがって
\(k=\displaystyle\frac{1}{a^2+b^2+c^2}\)
ゆえに\(H\)の座標は
\(H(\displaystyle\frac{a}{a^2+b^2+c^2},\displaystyle\frac{b}{a^2+b^2+c^2},\displaystyle\frac{c}{a^2+b^2+c^2})\)
また
\(OH=\sqrt{\displaystyle\frac{a^2+b^2+c^2}{(a^2+b^2+c^2)^2}}\)
\(=\displaystyle\frac{1}{\sqrt{a^2+b^2+c^2}}\)
(2)
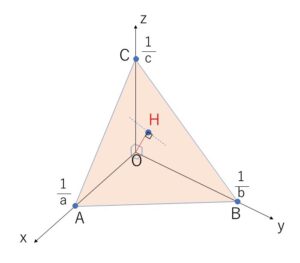
四面体\(OABC\)の体積を\(V\)とする。
底面を\(△OAB\)とすると
\(V=\displaystyle\frac{1}{3}(\displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{a}\cdot\displaystyle\frac{1}{b})\cdot\displaystyle\frac{1}{c}=\displaystyle\frac{1}{6abc}\)
また、底面を\(ABC\)とすると
\(V=\displaystyle\frac{1}{3}S\cdot OH\)
よって
\(S=3V\cdot\displaystyle\frac{1}{OH}\)
(\(OH=1\), \(c=\displaystyle\frac{1}{\sqrt{3}}\) より)
\(=\displaystyle\frac{\sqrt{3}}{2ab}\)・・・③
\(OH=1\) より(1)から
\(\displaystyle\frac{1}{\sqrt{a^2+b^2+c^2}}=1\)
よって
\(a^2+b^2+c^2=1\)
\(a^2+b^2=\displaystyle\frac{2}{3}\)・・・④
以下\(a,b\)が正の数であることに注意して
相加相乗平均の不等式から
\(\displaystyle\frac{a^2+b^2}{2}≧\sqrt{a^2b^2}=ab\)
となるので
\(ab≦\displaystyle\frac{1}{3}\)
したがって
\(\displaystyle\frac{1}{ab}≧3\)
ゆえに
\(S=\displaystyle\frac{\sqrt{3}}{2ab}\)\(≧\displaystyle\frac{3\sqrt{3}}{2}\)
等号成立は
\(a^2=b^2\) つまり \(a=b\) のときで
④より
\(a^2+a^2=\displaystyle\frac{2}{3}\)
よって \(a=b=\displaystyle\frac{1}{\sqrt{3}}\) のとき最小値をとる。
以上より\(S\)の最小値は
\(\displaystyle\frac{3\sqrt{3}}{2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→平面に下ろした垂線②(点と平面の距離) back→直線と平面の交点、直線と平面の平行