不等式を利用する(はさみうちの原理)を利用する、漸化式と極限の例題です。
(例題1)
\(a\)を正の定数とする。\(f(x)=x^2-a\) として、関数\(y=f(x)\)のグラフ上の点\((x_n,f(x_n))\)における接線が\(x\)軸と交わる点の\(x\)座標を\(x_{n+1}\)とする。このようにして、\(x_{1}\)から順に\(x_2,x_3,x_4,\cdots\)を作る。ただし、\(x_1>\sqrt{a}\)とする。
(1)\(x_{n+1}\)を\(x_n\)を用いて表せ。
(2)\(\sqrt{a}<x_{n+1}<x_n\) であることを示せ。
(3)\(|x_{n+1}-\sqrt{a}|<\displaystyle\frac{1}{2}|x_{n}-\sqrt{a}|\) であることを示せ。
(4)\(\displaystyle\lim_{n \to \infty}x_n\) を求めよ。
(解答)
(1)
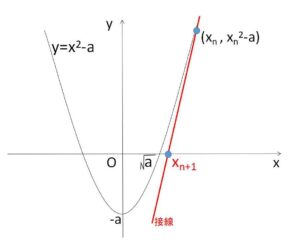
\(y=f(x)=x^2-a\)
\((x_n,x_n^2-a)\) における接線の方程式は、\(f'(x)=2x\) より
\(y=2x_n(x-x_n)+x_n^2-a\)
この接線の\(x\)切片が\(x_{n+1}\)だから
\(0=2x_n(x_{n+1}-x_n)+x_n^2-a\)
よって
\(2x_nx_{n+1}=x_n^2+a\)・・・①
ここで、\(x_n=0\) とすると ①は \(0=a\) となるが、\(a\)は正の定数だから不適。
ゆえに\(x_n≠0\)だから①の両辺を\(2x_n\)で割って
\(x_{n+1}=\displaystyle\frac{1}{2}x_n+\displaystyle\frac{a}{2x_n}\)
(2)
不等式の証明の基本は、各辺の差をとることですが、\(\sqrt{a}<x_n\) のほうは\(n\)が自然数であることと、漸化式が手に入っていることから帰納法で示していきます。
(ア)まず \(\sqrt{a}<x_{n}\) を数学的帰納法により示す。
(i)\(n=1\) のとき
条件から \(x_1>\sqrt{a}\) だから成立
(ii)\(n=k\) のとき (\(k=1,2,\cdots\))
\(\sqrt{a}<x_{k}\) が成り立つと仮定する。
このとき漸化式より
\(x_{k+1}-\sqrt{a}\)
\(=\displaystyle\frac{1}{2}x_k+\displaystyle\frac{a}{2x_k}-\sqrt{a}\)
\(=\displaystyle\frac{x_k^2+a-2\sqrt{a}x_k}{2x_{k}}\)
\(=\displaystyle\frac{(x_k-\sqrt{a})^2}{2x_{k}}>0\)
したがって \(\sqrt{a}<x_{k+1}\) であり、\(n=k+1\)でも成立する。
(i)(ii)より、任意の自然数\(n\)で \(\sqrt{a}<x_n\)
(イ)次に、\(x_{n+1}<x_n\) を示す。
\(x_{n}-x_{n+1}\)
\(=x_{n}-(\displaystyle\frac{1}{2}x_n+\displaystyle\frac{a}{2x_n})\)
\(=\displaystyle\frac{x_n^2-a}{2x_{n}}>0\) (∵(ア)より \(x_n^2>a\) )
よって \(x_{n+1}<x_n\)
(ア)(イ)より
\(\sqrt{a}<x_{n+1}<x_n\)
(3)
なおこの例題だと絶対値はあっても無くても変わりませんが、正負どちらにも対応できるように絶対値をつけることが多いです。
\(|x_{n+1}-\sqrt{a}|\)
\(=|\displaystyle\frac{1}{2}x_n+\displaystyle\frac{a}{2x_n}-\sqrt{a}|\)
\(=\left|\displaystyle\frac{(x_n-\sqrt{a})^2}{2x_{n}}\right|\)
\(=\left|\displaystyle\frac{x_n-\sqrt{a}}{2x_n}\right||x_n-\sqrt{a}|\)
\(=\displaystyle\frac{1}{2}\left|(1-\displaystyle\frac{\sqrt{a}}{x_n})\right||x_n-\sqrt{a}|\)
ここで(2)より \(x_n>\sqrt{a}\ (>0)\) だから
\(0<\displaystyle\frac{\sqrt{a}}{x_n}<1\)
よって
\(\left|(1-\displaystyle\frac{\sqrt{a}}{x_n})\right|<1\)
となるから
\(|x_{n+1}-\sqrt{a}|<\displaystyle\frac{1}{2}|x_n-\sqrt{a}|\)
(4)
\(a_n=2a_{n-1}=2^2a_{n-2}=2^3a_{n-3}=\cdots=2^{n-1}a_1\)
となります。これと同じことを不等式でもやります。(3)の不等式は両辺で1つずれた形になっているのでこの方法が使えます。
(3)より
\(|x_{n}-\sqrt{a}|<\displaystyle\frac{1}{2}|x_{n-1}-\sqrt{a}|\)
\(<\displaystyle\frac{1}{2^{2}}|x_{n-2}-\sqrt{a}|\)
\(<\displaystyle\frac{1}{2^{3}}|x_{n-3}-\sqrt{a}|\)
\(\cdots<\displaystyle\frac{1}{2^{n-1}}|x_1-\sqrt{a}|\)
よって
\(0<|x_n-\sqrt{a}|<\displaystyle\frac{1}{2^{n-1}}|x_1-\sqrt{a}|\)
ここで、(\(x_1\)は有限な値だから)
\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{2^{n-1}}|x_1-\sqrt{a}|=0\) であり、はさみうちの原理より
\(\displaystyle\lim_{n \to \infty}|x_n-\sqrt{a}|=0\)
したがって
\(\displaystyle\lim_{n \to \infty}x_n=\sqrt{a}\)
(例題2)
数列\(\{a_n\}\)を
\(a_1=1\), \(a_{n+1}=\sqrt{\displaystyle\frac{3a_n+4}{2a_n+3}}\) (\(n=1,2,3,\cdots\))
で定める。
(1)\(n≧2\) のとき、\(a_n>1\) となることを示せ。
(2)\(α^2=\displaystyle\frac{3α+4}{2α+3}\) を満たす正の実数\(α\)を求めよ。
(3)すべての自然数\(n\)に対して \(a_n<α\) となることを示せ。
(4)\(0<r<1\) を満たすある実数\(r\)に対して、不等式 \(\displaystyle\frac{α-a_{n+1}}{α-a_n}≦r\) (\(n=1,2,3,\cdots\)) が成り立つことを示せ。さらに、極限 \(\displaystyle\lim_{n \to \infty}a_n\) を求めよ。
(1)
\(a_{n+1}=\sqrt{\displaystyle\frac{3a_n+4}{2a_n+3}}=\sqrt{\displaystyle\frac{2a_n+3+a_n+1}{2a_n+3}}\)
\(=\sqrt{1+\displaystyle\frac{a_n+1}{2a_n+3}}\)・・・①
また \(a_1=1\) と漸化式より \(a_n>0\) がいえるので、①より
\(a_{n+1}>1\) (\(n=1,2,3,\cdots\))
したがって \(n≧2\) のとき、\(a_n>1\) となる。
(2)
(方程式を解くだけです)
\(α^2=\displaystyle\frac{3α+4}{2α+3}\) より (\(α>0\)より分母は正)
\(α^2(2α+3)=3α+4\)
\(2α^3+3α^2-3α-4=0\)
\((α+1)(2α^2+α-4)=0\)
\(α>0\) より
\(α=\displaystyle\frac{-1+\sqrt{33}}{4}\)
(3)
すべての自然数で \(a_n<α\) が成り立つことを数学的帰納法で示す。
(i)\(n=1\) のとき
\(a_1=1\)
\(α=\displaystyle\frac{-1+\sqrt{33}}{4}>\displaystyle\frac{-1+\sqrt{25}}{4}=1\) だから
\(a_1<α\) は成立。
(ii)\(n=k\) のとき (\(k=1,2,3,\cdots\))
\(a_k<α\) が成立すると仮定する。
このとき
\(α^2-a_{k+1}^2\)
\(=\displaystyle\frac{3α+4}{2α+3}-\displaystyle\frac{3a_k+4}{2a_k+3}\)
\(=\displaystyle\frac{α-a_k}{(2α+3)(2a_k+3)}>0\)・・・②
(∵ 仮定 \(a_k<α\) と、\(α>1\), \(a_k≧1\) より )
よって
\(a_{k+1}^2<α^2\) が成り立ち、\(α\)も\(a_{k+1}\)も正の数だから
\(a_{k+1}<α\)
ゆえに\(n=k+1\)でも成立する。
以上より、すべての自然数\(n\)に対して \(a_n<α\)
(4)
(3)の②で\(k\)を\(n\)にして
\(α^2-a_{n+1}^2=\displaystyle\frac{α-a_n}{(2α+3)(2a_n+3)}\)・・・③
左辺を因数分解すると\((α-a_{n+1})(α+a_{n+1})\) であり、
③の両辺を\((α-a_n)(α+a_{n+1})\ (≠0)\) で割ると
\(\displaystyle\frac{α-a_{n+1}}{α-a_n}=\displaystyle\frac{1}{(2α+3)(2a_n+3)(α+a_{n+1})}\)
ここで、\(α>1\), \(a_n≧1\), \(a_{n+1}>1\) だから
\((2α+3)(2a_n+3)(α+a_{n+1})>5\cdot5\cdot2=50\)
よって
\(\displaystyle\frac{α-a_{n+1}}{α-a_n}≦\displaystyle\frac{1}{50}\)・・・(注)
となるので、\(r=\displaystyle\frac{1}{50}\) とすれば
\(\displaystyle\frac{α-a_{n+1}}{α-a_n}≦r\)・・・④
が成り立つ。
イコールつきの不等号は、\(<\) と \(=\) のどちらか一方のみが成り立っていればよいので、\(≦\) としても問題ありません。
さらに④より、\(a_n<α\) だから (分母を払っても不等号の向きは変わらず)
\(α-a_{n+1}≦r(α-a_n)\) (1個ずれた形)
この不等式を繰り返し使うことで
\(0<α-a_n≦r^{n-1}(α-a_1)\)
が成り立つことになる。
\(0<r<1\) より
\(\displaystyle\lim_{n \to \infty}r^{n-1}(α-a_1)=0\)
だから、はさみうちの原理より
\(\displaystyle\lim_{n \to \infty}(α-a_n)=0\)
したがって
\(\displaystyle\lim_{n \to \infty}a_n=α=\displaystyle\frac{-1+\sqrt{33}}{4}\)
(参考)
\(a_{n+1}=f(a_n)\) 型の漸化式で一般的にいえることですが、\(y=f(x)\) と \(y=x\) のグラフを描くことにより、極限を予想することができます。
(例題2)では、\(a_{n+1}=\sqrt{\displaystyle\frac{3a_n+4}{2a_n+3}}\) なので、
\(f(x)=\sqrt{\displaystyle\frac{3x+4}{2x+3}}\)
とおくと、前の項を\(x\)座標とすると次の項が\(y=f(x)\)の\(y\)座標になるので、\(y=x\)上の点は\(x,y\)座標が等しいから、項を次々に求める作業は座標平面上での階段状の動きに対応します。すると、\(a_n\)は2つのグラフの交点の\(x(y)\)座標に向かうことが予想できます。(例題2)ではこの交点の\(x\)座標を(2)で求めています。
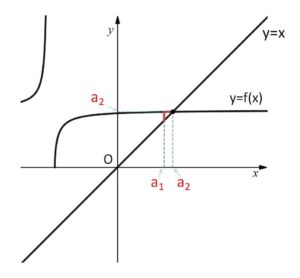
(かなり早い段階で交点に近づいています)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→無限級数の発散・収束① back→漸化式と極限②(分数型・連立型)