1次関数 \(y=ax+b\) の最大最小値は、\(a>0\)の場合\(x\)が増加すると\(y\)も増加し(単調増加)、\(a<0\)の場合\(x\)が増加すると\(y\)は減少する(単調減少)ので、最大最小値を求めるのは簡単です。しかし、2次関数の場合は、頂点を境目にして増加する領域と減少する領域が分かれているので、難易度が上がります。まずは簡単な例から考えていきましょう。
・2次関数の最大最小値 (定義域が実数全体)
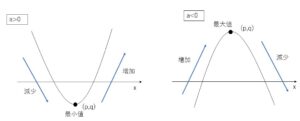
2次関数 \(y=ax^2+bx+c\)で 定義域が特に制限されていない(実数全体をとる)場合について考えていきます。グラフを考えるために標準形にした式を、\(y=a(x-p)^2+q\)とします。まず \(a>0\) の場合、最小値は頂点の\(y\)座標で、\(x=p\)における値\(q\)となります。最大値は、\(x\)を大きくすればいくらでも\(y\)の値は大きくなるので、存在しません。\(a<0\)の場合は、最小値は\(x\)を大きくすればいくらでも\(y\)の値は小さくなるので存在せず。最大値は頂点の\(y\)座標で、\(x=p\)における値\(q\)となります。
(例題1)
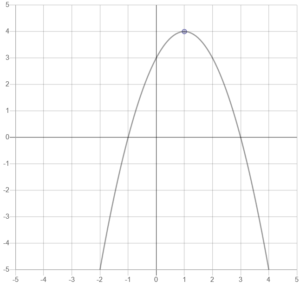
\(y=-x^2+2x+3\)の最大値と最小値とそのときの\(x\)の値を求めよ。
(解答)
平方完成して標準形にすると
\(y=-(x-1)^2+4\)
グラフより、最大値は \(4\) (\(x=1\))
最小値はない
・定義域が制限されている場合(具体例)
定義域が制限されている場合の一般論は難しいので、まず定義域が具体的に表されている場合について見ていきます。
(例題2)
次の変域における \(y=x^2-2x-3\) の最大値または最小値を求めよ。
(1) \(-1<x≦2\) (2) \(0≦x≦2\) (3)\(2≦x≦4\)
(解答)
平方完成して標準形にすると
\(y=(x-1)^2-4\)
(1)
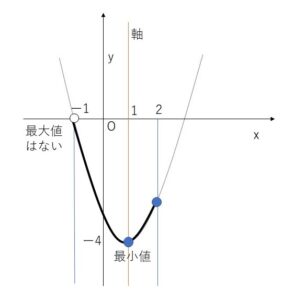
グラフは図の太線部分。
最小値は \(x=1\)のとき \(-4\)
最大値はない
(2)
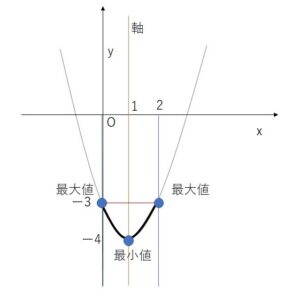
グラフより
最大値は \(x=0,2\) のとき \(-3\)
最小値は \(x=1\) のとき \(-4\)
(3)
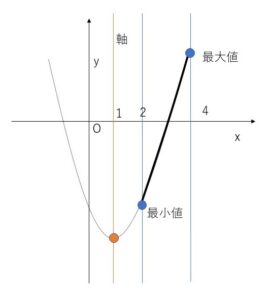
グラフより
最大値は\(x=2\)のとき \(-3\)
最大値は\(x=4\)のとき \(5\)
・定義域が制限されている場合(一般)
頂点を境目に増加する領域と減少する領域が分かれているので、軸と定義域の位置関係で場合分けしていきます。 \(y=a(x-p)^2+q\) で \(a>0\) の場合を考えていきます。
(定義域を \(h≦x≦i\) 最大値をM、最小値をmとします)
(1)軸が区間の右側にある場合
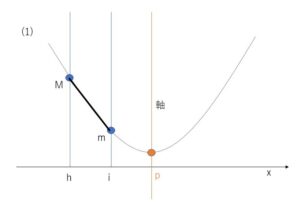
最大値は左端\(x=h\)、最小値は右端\(x=i\)での値です。
(2)軸が区間の中にあり、右寄りの場合
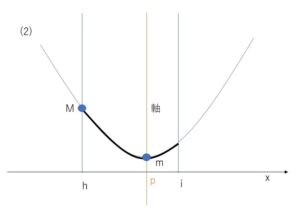
最大値は左端\(x=h\)、最小値は頂点\(x=p\)での値です。
(3)軸が区間の中にあり、ちょうど中央の場合
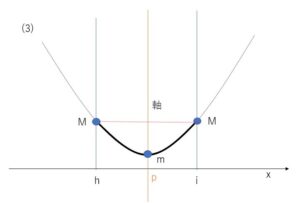
最大値は両端\(x=h,i\)、最小値は頂点\(x=p\)での値です。
(4)軸が区間の中にあり、左寄りの場合
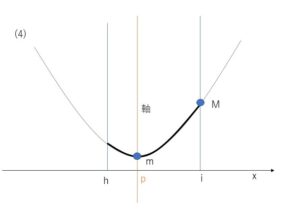
最大値は右端\(x=i\)、最小値は頂点\(x=p\)での値です。
(5)軸が区間の左側にある場合
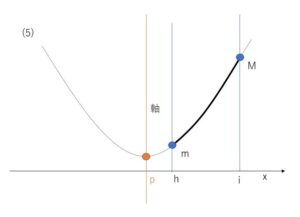
最大値は右端\(x=i\)、最小値は左端\(x=h\)での値です。