引き続き極方程式で表された曲線の概形について見ていきます。
今回はレム二スケートと呼ばれる曲線です。
・レム二スケート
極方程式
\(r^2=a^2\cos2θ\)・・・① (\(a>0\))
で表される曲線をレム二スケートと呼びます。\(r^2=2a^2\cos2θ\) の形で表されることもあります。
\(a=1\)として
\(r^2=\cos2θ\)・・・②
の曲線の概形を調べてみます。この曲線では\(θ\)の範囲(定義域)が制限されます。つまり①の左辺は \(r^2≧0\) であるため
\(\cos2θ≧0\)
という制限がつくことに注意です。したがって例えば \(0≦θ≦π\) の範囲で考えるならば、\(0≦θ≦\displaystyle\frac{π}{4}\)、\(\displaystyle\frac{3π}{4}≦θ≦π\) のみで考える必要が出てきます。
それでは対称性や周期性を調べてます。②を
\(F(r,θ)=r^2-\cos2θ=0\)
とおくと、
\(F(r,θ)=F(r,-θ)=F(-r,-θ)=F(-r,θ)=0\)
が成り立つので、「始線・極を通り始線に垂直な直線・極」について対称です。
続いて周期性ですが②で \(θ+π\) とすると
\(r^2=\cos2(θ+π)=\cos2θ\)
となり\(r\)が戻り、正の値 \(\cos2θ\) 1つに対して\(r\)が絶対値の同じ正負の値を1つずつとることから、周期\(π\)で繰り返しになるので \(0≦θ≦π\) の範囲だけ調べればよいことになります。
最初に検討したように、\(0≦θ≦\displaystyle\frac{π}{4}\)、\(\displaystyle\frac{3π}{4}≦θ≦π\) で調べると、グラフは次のようになります。
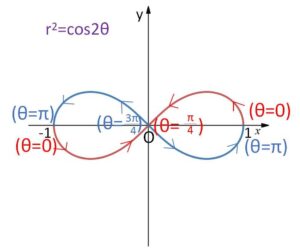
ところで、レム二スケートを直交座標の方程式で表してみると
\(r^2=a^2\cos2θ\)・・・①
より、
\(r^2=a^2(\cos^2θ-\sin^2θ)\)
両辺\(r^2\)倍して
\(r^4=a^2(r^2\cos^2θ-r^2\sin^2θ)\)
よって
\((x^2+y^2)^2=a^2(x^2-y^2)\)・・・③
(\(r^2=2a^2\cos2θ\) 型だと、右辺の係数が\(2a^2\)になる)
となり、③からも「\(x\)軸、\(y\)軸、原点」についての対称性を確認できます。
逆に③を極方程式に直すと
\(r^4=a^2(r^2\cos^2θ-r^2\sin^2θ)\)
\(r^4=a^2r^2\cos2θ\)
\(r^2(r^2-a^2\cos2θ)=0\)
より
\(r=0\) または \(r^2=a^2\cos2θ\)・・・①
となりますが、\(r=0\) は①に含まれるので (例えば\(θ=\displaystyle\frac{π}{4}\) など)
③と①は同じ曲線を表すことが分かります。(必要十分条件)
なお
楕円: 2定点からの距離の和が一定
双曲線: 2定点からの距離の差が一定
に対応させて、レム二スケートを「2定点からの距離の積が一定」となる点の軌跡と表現することもあります。
実際、\(a\)を正の定数として、2定点を \(A(a,0),\ B(-a,0)\) 、一定値を\(a^2\)とすると、軌跡上の点を \(P(x,y)\) として
\(AP\cdot BP=a^2\)
\(AP^2\cdot BP^2=a^4\)
\(\{(x-a)^2+y^2\}\{(x+a)^2+y^2\}=a^4\)
\(\{(x^2+y^2)-2ax+a^2\}\{(x^2+y^2)+2ax+a^2\}=a^4\)
\((x^2+y^2)^2+2a^2(x^2+y^2)-4a^2x^2+a^4=a^4\)
よってレム二スケート
\((x^2+y^2)^2=2a^2(x^2-y^2)\)
が導かれます。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→極方程式と曲線の概形③ back→極方程式と曲線の概形①