極座標を利用する例題です。
以下の例題でその便利さについて見ていきます。
(例題1)
楕円 \(\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1\) (\(a>b>0\)) 上に \(OP \perp OQ\) を満たしながら動く2点\(P,Q\)がある。ただし、\(O\)は原点である。このとき、\(\displaystyle\frac{1}{OP^2}+\displaystyle\frac{1}{OQ^2}\) は一定であることを示せ。
ただし円ではないので、\(O\)からの距離については\(r_1,r_2\)と別の変数で考えることに注意です。
(なお媒介変数で、\(P(a\cosθ,b\sinθ)\) とおいたとき、\(OP\)と\(x\)軸となす角は\(θ\)にならないので、\(Q(a\cos(θ+\displaystyle\frac{π}{2}),b\sin(θ+\displaystyle\frac{π}{2}))\) とやってはダメです) ( →(参照) )
(解答)
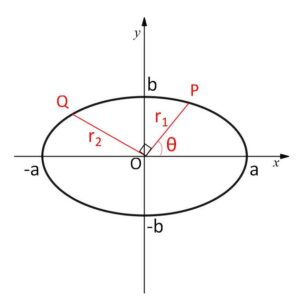
\(P,Q\)の位置を図のような順番にしても一般性を失わない。
\(P(r_1\cosθ,\ r_1\sinθ)\) とおくと、\(Q(r_2\cos(θ+\displaystyle\frac{π}{2}),\ r_2\sin(θ+\displaystyle\frac{π}{2}))\)
つまり、\(Q(-r_2\sinθ,\ r_2\cosθ)\)
\(P,Q\)は
楕円 \(\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1\) 上にあるから
\(r_1^2(\displaystyle\frac{\cos^2θ}{a^2}+\displaystyle\frac{\sin^2θ}{b^2})=1\)
\(r_2^2(\displaystyle\frac{\sin^2θ}{a^2}+\displaystyle\frac{\cos^2θ}{b^2})=1\)
したがって
\(\displaystyle\frac{1}{OP^2}+\displaystyle\frac{1}{OQ^2}\)
\(=\displaystyle\frac{1}{r_1^2}+\displaystyle\frac{1}{r_2^2}\)
\(=(\displaystyle\frac{\cos^2θ}{a^2}+\displaystyle\frac{\sin^2θ}{b^2})+(\displaystyle\frac{\sin^2θ}{a^2}+\displaystyle\frac{\cos^2θ}{b^2})\)
\(=\displaystyle\frac{1}{a^2}+\displaystyle\frac{1}{b^2}\) (一定)
(例題2)
座標平面上の点\((x,y)\)が
\((x^2+y^2)^2-(3x^2-y^2)y=0\) (\(x≧0,y≧0\))
で定まる集合上を動くとき、\(x^2+y^2\) の最大値、およびその最大値を与える\(x,y\)の値を求めよ。
点\((x,y)\)を、\((r\cosθ,r\sinθ)\) (\(r≧0\), \(0≦θ≦\displaystyle\frac{π}{2}\)) とおくと
\((x^2+y^2)^2-(3x^2-y^2)y=0\) より
\(r^4-(3r^2\cos^2θ-r^2\sin^2θ)\cdot r\sinθ=0\)
\(r^3(r-3\cos^2θ\sinθ+\sin^3θ)=0\)
よって
\(r=0\) または \(r=3\cos^2θ\sinθ-\sin^3θ\)・・・①
①は
\(r=3(1-\sin^2θ)\sinθ-\sin^3θ\)
\(=3\sinθ-4\sin^3θ\)
\(=\sin3θ\)
となるので、\(r=0\)を含む。
ゆえに題意を満たすような\(r,θ\)の関係式は
\(r=\sin3θ\) (正葉曲線)
このとき
\(x^2+y^2=r^2=\sin^23θ\)
\(r≧0\) より \(0≦3θ≦π\) だから、\(3θ=\displaystyle\frac{π}{2}\) のとき、最大値 \(1^2=1\) をとる。
また最大値をとるとき、\((r,θ)=(1,\displaystyle\frac{π}{6})\) であるから
\((x,y)=(1\cos\displaystyle\frac{π}{6}\ ,1\sin\displaystyle\frac{π}{6})\)
\(=(\displaystyle\frac{\sqrt{3}}{2},\displaystyle\frac{1}{2})\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
back→極方程式と曲線の概形③