図形を用いて 15°についての三角比を求めてみます。
(問題)
次の直角三角形の図を用いて、\(\sin15°,\cos15°,\tan15°\) の値を求めよ。
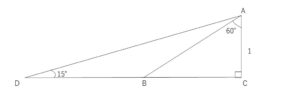
(解答)
\(\angle ABC=30°\) より
\(BA=2\) \(BC=\sqrt{3}\)
また \(\angle DAC=90°-15°=75°\) より \(\angle DAB=15°\)
よって三角形\(BAD\)は、\(BA=BD\)の二等辺三角形。
したがって、\(BD=BA=2\)
さらに三角形\(ADC\)において三平方の定理より
\(AD=\sqrt{DC^2+CA^2}\)
\(=\sqrt{(2+\sqrt{3})^2+1^2}\)
\(=\sqrt{8+4\sqrt{3}}\)
\(=\sqrt{8+2\sqrt{12}}\)
\(=\sqrt{6+2+2\sqrt{12}}\)
\(=\sqrt{(\sqrt{6}+\sqrt{2})^2}\)
\(=\sqrt{6}+\sqrt{2}\)
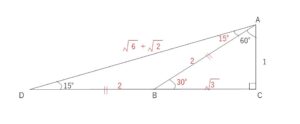
以上から
\(\sin15°=\displaystyle\frac{AC}{AD}\)
\(=\displaystyle\frac{1}{\sqrt{6}+\sqrt{2}}\)\(=\displaystyle\frac{\sqrt{6}-\sqrt{2}}{(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2})}\)\(=\)\(\displaystyle\frac{\sqrt{6}-\sqrt{2}}{4}\)
\(\cos15°=\displaystyle\frac{DC}{AD}\)
\(=\displaystyle\frac{2+\sqrt{3}}{\sqrt{6}+\sqrt{2}}\)\(=\displaystyle\frac{(2+\sqrt{3})(\sqrt{6}-\sqrt{2})}{(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2})}\)\(=\)\(\displaystyle\frac{\sqrt{6}+\sqrt{2}}{4}\)
\(\tan15°=\displaystyle\frac{AC}{DC}\)
\(=\displaystyle\frac{1}{2+\sqrt{3}}\)\(=\displaystyle\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}=\)\(2-\sqrt{3}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。