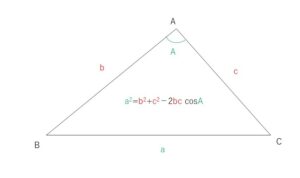
余弦定理について見ていきます。名前の通り、\(\cos\)が登場する定理です。
・余弦定理
\(△ABC\)において、次の余弦定理が成り立ちます。
\(a^2=b^2+c^2-2bc\cos A\)
\(b^2=c^2+a^2-2ca\cos B\)
\(c^2=a^2+b^2-2ab\cos C\)
私の個人的な覚え方ですが、一番上の式の場合、まず角\(A\)とその対辺\(a\)着目して、対辺の\(2\)乗 \(a^2=\) の右辺は、「(角を挟む辺\(b,c\)の\(2\)乗の和)\(-2×\)(角を挟む辺\(b,c\)の積)×(\(\cos\)挟まれる角\(A\))」として図形と照らし合わせて覚えています。

また、それぞれの式を変形すると
\(\cos A=\displaystyle\frac{b^2+c^2-a^2}{2bc}\)
\(\cos B=\displaystyle\frac{c^2+a^2-b^2}{2ca}\)
\(\cos C=\displaystyle\frac{a^2+b^2-c^2}{2ab}\)
が導かれる。
(証明)
まず、\(a^2=b^2+c^2-2bc\cos A\)・・・(※) について証明する。
(1)\(A,B\)がともに鋭角の場合
図のように、\(△ABC\)の頂点\(A\)が原点、辺\(AB\)が\(x\)軸の正の部分にあるように座標軸を定める。ただし\(C\)は第一象限にあるとする。
考えやすくするために座標軸を設定します。ここで\(A\)を原点、\(AB\)を\(x\)軸の正の部分に置くという限定された設定をしていますが、これで問題ありません。\(A,B\)を鋭角とする三角形\(ABC\)は山ほどありますが、それらの三角形を\(AB\)を下側に水平にして\(A\)を原点に置いているだけなので、形は全く変えずにそのままで移動させていることになるからです。また、このように座標設定することで、\(A,B\)が鋭角の任意の三角形を表すことができたことになります。(\(A\)は固定されていて\(B,C\)が変数の値によって動いて色々な三角形ができるイメージ)
頂点\(B,C\)の座標はそれぞれ、\(B(c,0)\), \(C(b\cos A,b\sin A)\)となる。
点\(C\)から\(x\)軸に垂線を下ろし、その足を\(H\)とすると
点\(C\)から\(x\)軸に垂線を下ろし、その足を\(H\)とすると
\(BC^2=BH^2+CH^2\)・・・①
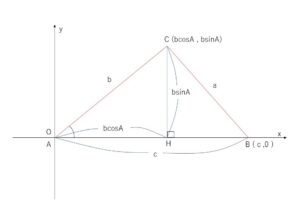
\(BC=a\), \(BH=AB-AH=c-b\cos A\), \(CH=b\sin A\) を①に代入して
\(a^2=(c-b\cos A)^2+(b\sin A)^2\)・・・②
展開して整理すると
\(a^2=b^2(\sin^2 A+\cos^2A)+c^2-2bc\cos A\)
\(a^2=(c-b\cos A)^2+(b\sin A)^2\)・・・②
展開して整理すると
\(a^2=b^2(\sin^2 A+\cos^2A)+c^2-2bc\cos A\)
よって
\(a^2=b^2+c^2-2bc\cos A\)・・・(※)
\(a^2=b^2+c^2-2bc\cos A\)・・・(※)
(2)\(90°≦B<180°\)の場合
(1)と同様に考えると、図は次のとおり。
(1)と同様に考えると、図は次のとおり。
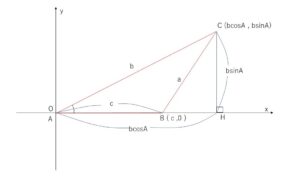
ここで \(BC=a\), \(BH=AH-AB=b\cos A-c\), \(CH=b\sin A\)
\(BC^2=BH^2+CH^2\) に代入すると
\(a^2=(b\cos A-c)^2+(b\sin A)^2\)
これは②と同じ式なので、結局(※)は成り立つ。
\(BC^2=BH^2+CH^2\) に代入すると
\(a^2=(b\cos A-c)^2+(b\sin A)^2\)
これは②と同じ式なので、結局(※)は成り立つ。
(3)\(90°≦A<180°\)の場合
(1)と同様に考えると。図は次のとおり。
(1)と同様に考えると。図は次のとおり。
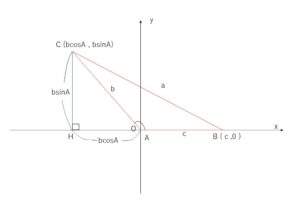
ここで \(BC=a\), \(BH=AB+AH=c-b\cos A\), \(CH=b\sin A\)
\(BC^2=BH^2+CH^2\) に代入すると
\(a^2=(c-b\cos A)^2+(b\sin A)^2\)
これは②の式そのままなので、結局(※)は成り立つ。
\(BC^2=BH^2+CH^2\) に代入すると
\(a^2=(c-b\cos A)^2+(b\sin A)^2\)
これは②の式そのままなので、結局(※)は成り立つ。
以上(1)~(3)より、\(a^2=b^2+c^2-2bc\cos A\)
また、同様に次の2つの等式も成り立つ。
\(b^2=c^2+a^2-2ca\cos B\)
\(c^2=a^2+b^2-2ab\cos C\)
\(b^2=c^2+a^2-2ca\cos B\)
\(c^2=a^2+b^2-2ab\cos C\)
(例題1)
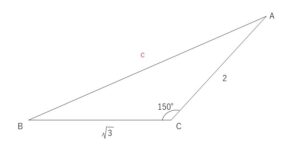
\(△ABC\)において、\(a=\sqrt{3}\), \(b=2\), \(C=150°\) のとき\(c\)を求めよ。
2辺とその挟む角が分かっているので、余弦定理を使います。
(解答)
余弦定理より
\(c^2=(\sqrt{3})^2+2^2-2・\sqrt{3}・2・\cos150°\)
よって \(c^2=13\)
\(c>0\) より \(c=\sqrt{13}\)
余弦定理より
\(c^2=(\sqrt{3})^2+2^2-2・\sqrt{3}・2・\cos150°\)
よって \(c^2=13\)
\(c>0\) より \(c=\sqrt{13}\)
(例題2)
\(△ABC\)において、\(a=8,b=5,c=7\) のとき\(C\)を求めよ。
3辺が分かっているので、余弦定理を変形した式
\(\cos C=\displaystyle\frac{a^2+b^2-c^2}{2ab}\)を使います。
\(\cos C=\displaystyle\frac{a^2+b^2-c^2}{2ab}\)を使います。
(解答)
\(\cos C=\displaystyle\frac{8^2+5^2-7^2}{2・8・5}=\displaystyle\frac{1}{2}\)
\(0°<C<180°\) だから、\(C=60°\)
(例題3)
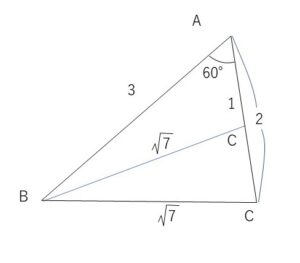
\(△ABC\)において、\(a=\sqrt{7}\), \(c=3\), \(A=60°\) のとき \(b\)を求めよ。
角を挟む辺が未知数\(b\)ですが、2辺と1角が分かっているので余弦定理を使って\(b\)の2次方程式を解きます。
(解答)
余弦定理より
\((\sqrt{7})^2=b^2+3^2-2・b・3\cos60°\)
整理すると
\(b^2-3b+2=0\) \((b-1)(b-2)=0\)より
\(b=1,2\)
余弦定理より
\((\sqrt{7})^2=b^2+3^2-2・b・3\cos60°\)
整理すると
\(b^2-3b+2=0\) \((b-1)(b-2)=0\)より
\(b=1,2\)
図より、2つの数どちらも答えになります。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
→高校数学TOP next→三角形の辺と角の決定 back→正弦定理の証明とその利用