2倍角の公式と同様に、加法定理を用いて3倍角の公式を導いていきます。
・3倍角の公式
3倍角の三角関数について次の公式が成り立ちます。
① \(\sin3α\)\(=3\sinα-4\sin^3α\)
② \(\cos3α\)\(=4\cos^3α-3\cosα\)
(証明)
\(\sin3α\)
\(=\sin(α+2α)\)
\(=\sinα\cos2α\)\(+\cosα\sin2α\)
\(=\sinα(1-2\sin^2α)\)\(+\cosα・2\sinα\cosα\)
\(=\sinα-2\sin^3α\)\(+2\sinα(1-\sin^2α)\)
\(=3\sinα-4\sin^3α\)
\(\cos3α\)
\(=\cos(α+2α)\)
\(=\cosα\cos2α\)\(-\sinα\sin2α\)
\(=\cosα(2\cos^2α-1)\)\(-\sinα・2\sinα\cosα\)
\(=2\cos^3α-\cosα\)\(-2\cosα(1-\cos^2α)\)
\(=4\cos^3α-3\cosα\)
万が一忘れても加法定理よりすぐに導けます。
なお、\(\tan3α\) については例題で扱いますが、こちらはあまり使わないです。
(例題1)
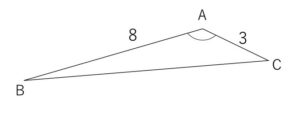
\(△ABC\)において \(AB=8\), \(AC=3\), \(\cos\displaystyle\frac{A}{3}\)\(=\displaystyle\frac{3}{4}\) のとき、辺\(BC\)の長さを求めよ。
\(\cos A\) は \(\cos\displaystyle\frac {A}{3}\) を用いて3倍角の公式を使って求めます。
余弦定理より
\(BC^2=8^2+3^2-2・8・3\cos A\)\(=73-48\cos A\)
また
\(\cos A\)\(=\cos(3・\displaystyle\frac{A}{3})\)\(=4\cos^3\displaystyle\frac{A}{3}-3\cos\displaystyle\frac{A}{3}\)
\(=4(\displaystyle\frac{3}{4})^3-3・\displaystyle\frac{3}{4}\)
\(=-\displaystyle\frac{9}{16}\)
よって
\(BC^2=73-48・(-\displaystyle\frac{9}{16})\)\(=100\)
\(BC=10\)
(例題2)
(1) \(0<2x<\displaystyle\frac{π}{4}\), \(\sin4x=\displaystyle\frac{24}{25}\) のとき、\(\sin2x+\cos2x\) の値を求めよ。
(2) \(\tan3θ\) を \(\tanθ\) で表せ。
(3) \(\sin5θ\) を \(\sinθ\) で表せ。
(解答)
(1)
この形が出で来るように、\(\sin2x+\cos2x\) を2乗します。
最後に平方根をとるときには、正負を吟味します。
\(\sin4x\)\(=2\sin2x\cos2x\) より
\(2\sin2x\cos2x\)\(=\displaystyle\frac{24}{25}\)
また
\((\sin2x+\cos2x)^2\)
\(=\sin^22x+\cos^22x\)\(+2\sin2x\cos2x\)
\(=1+\displaystyle\frac{24}{25}\)
\(=\displaystyle\frac{49}{25}\)
\(0<2x<\displaystyle\frac{π}{4}\) より
\(\sin2x>0\), \(\cos2x>0\) だから
\(\sin2x+\cos2x\)\(=\displaystyle\frac{7}{5}\)
(2)
\(\tan3θ\)
\(=\tan(θ+2θ)\)
\(=\displaystyle\frac{\tanθ+\tan2θ}{1-\tanθ\tan2θ}\)
\(=\displaystyle\frac{\tanθ+\displaystyle\frac{2\tanθ}{1-\tan^2θ}}{1-\tanθ\cdot\displaystyle\frac{2\tanθ}{1-\tan^2θ}}\)
(分母分子に \(1-\tan^2θ\) を掛けて)
\(=\displaystyle\frac{\tanθ(1-\tan^2θ)+2\tanθ}{(1-\tan^2θ)-2\tan^2θ}\)
\(=\displaystyle\frac{-\tan^3θ+3\tanθ}{1-3\tan^2θ}\)
\(=\)\(\displaystyle\frac{\tan^3θ-3\tanθ}{3\tan^2θ-1}\)
(3)
\(\sin5θ\)
\(=\sin(2θ+3θ)\)
\(=\sin2θ\cos3θ\)\(+\cos2θ\sin3θ\)
\(=2\sinθ\cosθ\)\((4\cos^3θ-3\cosθ)\)\(+(1-2\sin^2θ)\)\((3\sinθ\)\(-4\sin^3θ)\)
\(=2\sinθ\cos^2θ\)\((4\cos^2θ-3)\)\(+\sinθ(1-2\sin^2θ)\)\((3\)\(-4\sin^2θ)\)
\(=2\sinθ(1-\sin^2θ)\)\(\{4(1-\sin^2θ)\)\(-3\}\)
\(+\sinθ(1-2\sin^2θ)\)\((3\)\(-4\sin^2θ)\)
(見やすくするために \(\sinθ=x\) とおくと)
\(=2x(1-x^2)\)\(\{4(1-x^2)-3\}\)\(+x(1-2x^2)\)\((3-4x^2)\)
\(=2x(1-x^2)(1-4x^2)\)\(+x(1-2x^2)\)\((3-4x^2)\)
\(=2x(4x^4-5x^2+1)\)\(+x(8x^4-10x^2\)\(+3)\)
\(=16x^5-20x^3+5x\)
よって
\(\sin5θ\)\(=16\sin^5θ\)\(-20\sin^3θ\)\(+5\sinθ\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角方程式・不等式(倍角の公式) back→2倍角・半角の公式