特殊な角 \(72°,54°,36°,18°\) (\(\displaystyle\frac{2π}{5},\displaystyle\frac{3π}{10},\)\(\displaystyle\frac{π}{5},\displaystyle\frac{π}{10}\)) の三角関数の値の求め方について見ていきます。
(例題)
(1)\(\cos36°\) の値を求めよ。
(2)\(\sin18°\) の値を求めよ。
(3)\(\cos72°\) の値を求めよ。
(4)\(\sin54°\) の値を求めよ。
(i)\(θ(=36°)\)に関する方程式を作って方程式を解く
(ii)図形的に解く
の2パターンについて紹介します。
(解答)
(i)\(θ\)に関する方程式を作る方法
(1)
\(36°\)を5倍すると、ちょうど\(180°\)というキレイな値になります。これを利用して、\(θ=36°\) とおくと、\(5θ=180°\)。
\(5θ=3θ+2θ\) と分けて、\(3θ=180-2θ\)・・・(X)
あとは(X)の両辺について\(\cos\)ととるだけです。(\(\sin\)ととってもできます)
\(θ=36°\) とおく。
\(5θ=180°\) だから
\(3θ=180°-2θ\)
両辺 \(\cos\)をとると
\(\cos3θ=\cos(180°-2θ)\)
\(\cos3θ=-\cos(-2θ)\)
よって
\(\cos3θ=-\cos2θ\)
\(4\cos^3θ-3\cosθ\)\(=-(2\cos^2θ-1)\)
整理して
\(4\cos^3θ+2\cos^2θ-3\cosθ\)\(-1\)\(=0\)・・・①
\(\cosθ=-1\) と見つかります。よって因数定理より \((\cosθ+1)\) という因数をもちます。
\(\cosθ=-1\) は①を満たすので
\((\cosθ+1)\)\((4\cos^2θ-2\cosθ-1)\)\(=0\)
よって \(\cosθ=-1,\displaystyle\frac{1±\sqrt{5}}{4}\)
このどれかが答えになるわけですが、第1象限の角なので \(\cos36°>0\) より
\(\cos36°=\displaystyle\frac{1+\sqrt{5}}{4}\) に決定します。
\(\cosθ=\cos36°>0\) より
\(\cosθ=\)\(\cos36°=\displaystyle\frac{1+\sqrt{5}}{4}\)
(2)(3)
\(18°×5=90°\), \(72°×5=360°\) となり全く同じように解けます。
ですが、せっかく(1)で\(\cos36°\) の値を求めたので2倍角や半角の公式を使ってサクッと求めます。
\(\sin^218°=\displaystyle\frac{1-\cos36°}{2}\)
(1)の結果から
\(\sin^218°\)\(=\displaystyle\frac{1-\displaystyle\frac{1+\sqrt{5}}{4}}{2}\)
\(\sin^218°\)\(=\displaystyle\frac{3-\sqrt{5}}{8}\)
\(\sin18°>0\) だから
\(\sin18°\)\(=\sqrt{\displaystyle\frac{3-\sqrt{5}}{8}}\)
\(\sin18°\)\(=\sqrt{\displaystyle\frac{6-2\sqrt{5}}{16}}\)
\(\sin18°\)\(=\sqrt{\displaystyle\frac{(\sqrt{5}-1)^2}{16}}\)
したがって
\(\sin18°\)\(=\displaystyle\frac{\sqrt{5}-1}{4}\)
また
\(\cos72°=2\cos^236°-1\)
\(\cos72°\)\(=2(\displaystyle\frac{1+\sqrt{5}}{4})^2-1\)
右辺を計算して
\(\cos72°\)\(=\displaystyle\frac{\sqrt{5}-1}{4}\)
(4)
\(\sin54°\)\(=\sin(90°-36°)=\cos36°\)\(=\displaystyle\frac{1+\sqrt{5}}{4}\)
次に図形的に解く方法です。
内角 \(36°,72°,72°\) の二等辺三角形を考えることがポイントとなります。
(ii)図形的に解く方法
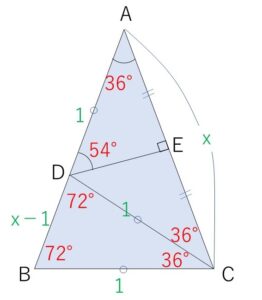
(1)
図のような底辺\(BC\)の大きさが1で、内角が \(36°,72°,72°\) の二等辺三角形を考える。
\(\angle C\) の2等分線を引いて\(AB\)との交点を\(D\)とする。
すると \(\angle CDB=72°\) だから
\(△CBD\) は二等辺三角形。
また、\(\angle ACD=36°\)より \(△DCA\) も二等辺三角形。
よって \(BC=CD=AD=1\)
ここで、\(△ABC\)と\(△CDB\) は相似だから
\(AC=AB=x\) とおくと
\(x:1=1:x-1\)
\(x(x-1)=1\)
\(x^2-x-1=0\)
\(x=\displaystyle\frac{1±\sqrt{5}}{2}\)
\(x>0\) より
\(x=\displaystyle\frac{1+\sqrt{5}}{2}\)
さらに \(D\)から\(AC\)に垂線\(DE\)を下ろすと、\(△DCA\)は二等辺三角形だから
\(AE=\displaystyle\frac{x}{2}\)
直角三角形\(ADE\) に着目して
\(\cos36°=\displaystyle\frac{\displaystyle\frac{x}{2}}{1}\)
したがって
\(\cos36°\)\(=\displaystyle\frac{x}{2}\)\(=\displaystyle\frac{1+\sqrt{5}}{4}\)
先に(4)を解くと
\(\angle ADE=54°\) より
\(\sin54°=\displaystyle\frac{\displaystyle\frac{x}{2}}{1}\)\(=\displaystyle\frac{x}{2}\)
よって
\(\sin54°\)\(=\displaystyle\frac{1+\sqrt{5}}{4}\)
(2)(3)
すると、内角\(18°,72°\) の直角三角形ができます。
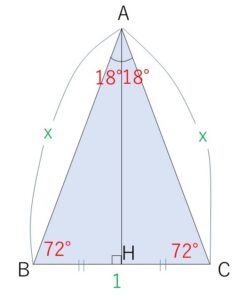
\(A\)から底辺\(BC\)に垂線\(AH\)をおろす。
\(\angle BAH=18°\), \(BH=\displaystyle\frac{1}{2}\) だから
\(\sin18°=\displaystyle\frac{\displaystyle\frac{1}{2}}{x}\)\(=\displaystyle\frac{1}{2x}\)
よって
\(\sin18°\)\(=\displaystyle\frac{1}{2}・\displaystyle\frac{2}{1+\sqrt{5}}\)\(=\displaystyle\frac{\sqrt{5}-1}{4}\)
\(\cos72°\)\(=\displaystyle\frac{\displaystyle\frac{1}{2}}{x}\)\(=\displaystyle\frac{1}{2x}\) より
\(\cos72°=\displaystyle\frac{\sqrt{5}-1}{4}\)
\(\sin36°=\cos54°\)\(=\displaystyle\frac{\sqrt{10-2\sqrt{5}}}{4}\)
\(\cos18°=\sin72°\)\(=\displaystyle\frac{\sqrt{10+2\sqrt{5}}}{4}\)
となります。(2重根号は外せません)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→積和・和積の公式 back→三角方程式・不等式(倍角の公式)