\(n\)進数の四則演算について学んでいきます。解き方は
①\(n\)進数のまま計算する ②普段使い慣れている\(10\)進数に直して計算する
の2パターンの方法があります。
(例題)
次の計算をせよ。
(1)\(1011_{(2)}+101_{(2)}\) (答えは2進法で表せ)
(2)\(3211_{(4)}-2312_{(4)}\) (答えは4進法で表せ)
(3)\(206_{(7)}×35_{(7)}\) (答えは7進法で表せ)
(4)\(110001_{(2)}÷111_{(2)}\) (答えは2進法で表せ)
まずは\(n\)進数のまま計算してみます。
(解答)
(1)
\(2\)進数では、各位が\(2\)以上になると桁数が上がります。
よって、和が\(1\)以下なら\(10\)進数の計算方法と同じで、\(2\)以上となっても、\(2\)が1つに対して位が1つ上の\(1\)となるだけなので、位上げに注意する以外は\(10\)進数と計算方法は変わりません。\(3\)進数、\(4\)進数・・・でも同様です。
\(1+1=2\) で位が上がるので

答え \(10000_{(2)}\)
(2)
ただし、1桁上の数\(1\)を借りてくるときに、\(n\)進法では\(n\)となることに注意してください。(2)では\(4\)進法なので、\(1\)を借りてくると、それは\(10\)ではなく、\(4\)です。
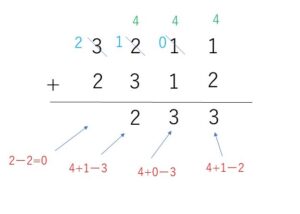
答えは \(233_{(4)}\)
(3)

答えは \(10612_{(7)}\)
(4)
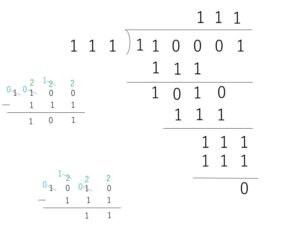
答えは \(111_{(2)}\)
※10進数に直して計算すると
(1)
\(1011_{(2)}=1・2^3+0・2^2+1・2^1+1\)\(=11\)
\(101_{(2)}=1・2^2+0・2^1+1\)\(=5\) より
\(1011_{(2)}+101_{(2)}\)\(=11+5=16\)
\(16\) を\(2\)進数にすると
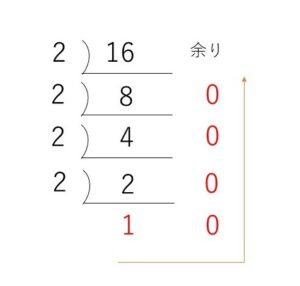
よって、答えは\(10000_{(2)}\)
(2)~(4)は結果のみ載せておてきます。
(2)
\(3211_{(4)}-2312_{(4)}\)\(=229-182=47=\)\(233_{(4)}\)
(3)
\(206_{(7)}×35_{(7)}\)\(=104×26=2704=\)\(10612_{(7)}\)
(4)
\(110001_{(2)}÷111_{(2)}\)\(=49÷7=7=\)\(111_{(2)}\)
以上です。お疲れさまでした。
ここまで見て頂きありがとうございました。