指数関数を含む関数の最大最小問題について見ていきます。
ポイントは置き換えなどを使って、見慣れた関数にすることです。
(例題1)
\(0≦x≦3\) のとき、
関数 \(y=4^{x+1}-2^{x+5}+56\)
の最大値と最小値、そのときの\(x\)の値を求めよ。
(解答)
なので、\(2^x=t\) と置き換えるとただの2次関数です。ただし置き換えたので、\(t\)の範囲に注意します。
\(y=4^{x+1}-2^{x+5}+56\)
\(=4\cdot4^x-2^5\cdot2^x+56\)
\(=4\cdot2^{2x}-32\cdot2^x+56\)
ここで \(t=2^{x}\) とおくと
\(0≦x≦3\) より、\(1≦t≦8\) で
\(y=4t^2-32t+56\)
\(=4(t-4)^2-8\)
最大値は、\(t=8\)のほうが、軸\(t=4\)より遠い位置にあるので、右端の\(t=8\) のときが最大値となります。(分からなかったら\(t=1,8\)のときを計算して比べてください)
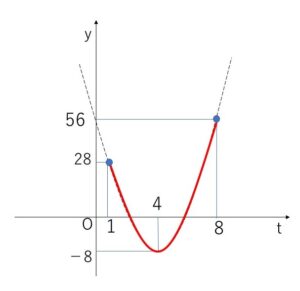
したがって
最小値は \(t=4\) のとき \(-8\)
このとき \(t=2^x=4\) より、\(x=2\)
最大値は \(t=8\) のとき、\(56\)
このとき、\(t=2^x=8\) より、 \(x=3\)
(例題2)
すべての実数\(x\)に対して定義された
関数 \(f(x)=4^x-2(2^x+2^{-x})+4^{-x}\)
の最小値と、そのときの\(x\)の値を求めよ。
\(t=2^x+2^{-x}\) と置き換えると、
\(4^{x}+4^{-x}=2^{2x}+2^{-2x}\) は、ちょうど指数のところが2倍になっている同じ形なので、\(t^2\)を計算することで、\(f(x)\)を\(t\)のみで表すことができます。
(解答)
\(t=2^x+2^{-x}\) とおくと
\(t^2\)\(=(2^x+2^{-x})^2\)
\(=4^x+2\cdot2^x\cdot2^{-x}+4^{-x}\)
\(=4^x+4^{-x}+2\)
だから
\(f(x)\)
\(=4^x+4^{-x}-2(2^x+2^{-x})\)
\(=t^2-2-2t\)
\(=(t-1)^2-3\)
\(t=2^x+\displaystyle\frac{1}{2^x}\) は逆数の和になっていて、\(2^x>0\), \(\displaystyle\frac{1}{2^x}>0\) だから、相加相乗平均を用います。
ここで、\(2^x>0\), \(\displaystyle\frac{1}{2^x}>0\) だから、相加相乗平均の不等式より
\(t=2^x+\displaystyle\frac{1}{2^x}\)
\(≧2\sqrt{2^x\cdot\displaystyle\frac{1}{2^x}}\)
\(=2\)
よって \(t≧2\)
等号は \(2^x=\displaystyle\frac{1}{2^x}\)
つまり
\((2^x)^2=1\)
\(4^x=1\)
\(x=0\) のとき。
2次関数 \(y=(t-1)^2-3\) (\(t≧2\))
を考えると、\(t≧2\) で増加関数なので、\(t=2\)で最小値 \(-2\) をとる。
このとき、相加相乗平均の不等式の等号が成り立つときなので、\(x=0\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→指数方程式の解の個数 back→指数不等式