対数の定義と、対数について成り立つ公式について学んでいきます。
・対数の定義
指数方程式 \(2^p=64\) や \(5^p=\sqrt[4]{5}\) の実数解はそれぞれ、\(p=6,\displaystyle\frac{1}{4}\)と簡単に求まりますが、\(2^p=3\) などはそうはいきません。
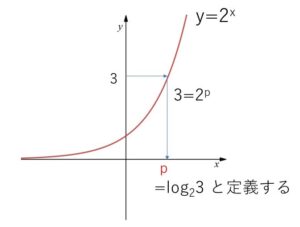
\(2^p=3\)・・・① について
指数関数のグラフ \(y=2^x\) を考えると、\(y=3\) に対応する\(x\)はただ1つだけ存在するので、等式①を満たす実数\(p\)はただ1つだけ存在することになります。そこで①を満たすただ1つの実数\(p\)を次のように \(\log\) (ログ) という記号と底\(2\)と累乗後の数\(3\)を用いて表します。
\(p=\log_{2}3\)
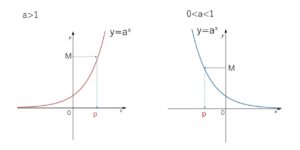
同様に一般的に、\(a>0\), \(a≠1\) とするとき、指数関数 \(y=a^x\) のグラフより、任意の正の実数\(M\)について、
\(a^{p}=M\)
となる実数\(p\)がただ1つ定まり、この\(p\)を
\(p=\log_{a}M\)
と表し、この\(p\)を底\(a\)とする\(M\)の対数とよびます。また、\(M\)を対数\(\log_{a}M\)の真数とよびます。
\(a>0\), \(a≠1\), \(M>0\) のとき
\(a^p=M\) ⇔ \(p=\log_{a}M\)
※指数関数と対数(関数)の構造を比べると、
\(2^p=3\)・・・(A) と \(p=\log_{2}3\)・・・(B) について
(A)指数「\(2\)を\(p\)乗すると→\(3\)になる」
(B)対数「\(2\)を何乗すると\(3\)になるか→\(p\)乗である」
ということになります。指数(関数)は累乗した結果に着目していて、対数は累乗した結果\(3\)が分かっている場合に何乗したかということに着目しています。よってこの2つ(A)(B)は着目する視点が変わっているだけで全く同じことを表していることになります。(同値なので\(⇔\)で結ばれている)
また、\(a\)と\(M\)の条件は対数の定義の出発点が指数関数なので、指数関数のときと同じように、底\(a\)については\(1\)ではない正の数、真数\(M\)については累乗後の数なので正の数ということになります。このうち特に問題を解くうえでは \(M>0\) のほうの条件が大事になってきます。(真数条件という)
・対数の性質
累乗 \(a^p\)について
\(a^0=1\), \(a^1=a\)
となるので、
\(\log_{a}1=0\)・・・① \(\log_{a}a=1\)・・・②
が成り立ちます。
また、\(a^p\)が、「\(a\)を\(p\)乗したもの」を意味することから
\(\log_{a}a^{p}=p\)
が成り立つことになり、\(p=0,1\)を代入することで①②を得ることもできます。
\(\log_{a}1=0\), \(\log_{a}a=1\)
次に対数の定義
\(a^p=M\)・・・(A) \(p=\log_{a}M\)・・・(B)
より、(B)を(A)に代入することで次の等式が得られます。
\(a^{\log_{a}M}=M\)
\(a^{\log_{a}M}=M\)
また、指数法則と対数の定義により、次の等式が成り立つことになります。
\(M,N\)を正の数、\(a\)を\(1\)でない正の数、\(r\)を実数とするとき
(1)\(\log_{a}MN=\log_{a}M+\log_{a}N\) (積→和)
(2)\(\log_{a}\displaystyle\frac{M}{N}=\log_{a}M-\log_{a}N\) (商→差)
特に \(M=1\) のとき \(\log_{a}\displaystyle\frac{1}{N}=-\log_{a}N\)
(3)\(\log_{a}M^{r}=r\log_{a}M\) (r乗→r倍)
特に \(\log_{a}\sqrt[r]{M}=\displaystyle\frac{1}{r}\log_{a}M\)
(証明)
\(\log_{a}M=p\), \(\log_{a}N=q\) とおくと、
\(a^p=M\), \(a^q=N\)
(1)
\(MN=a^{p}a^{q}=a^{p+q}\) (積は指数の和になる)
よって対数の定義から
\(\log_{a}MN=p+q\)
\(=\log_{a}M+\log_{a}N\)
(2)
\(\displaystyle\frac{M}{N}=\displaystyle\frac{a^{p}}{a^{q}}=a^{p-q}\) (商は指数の差になる)
よって対数の定義から
\(\log_{a}\displaystyle\frac{M}{N}=p-q\)
\(=\log_{a}M-\log_{a}N\)
\(M=1\) とすれば、\(\log_{a}1=0\) より
\(\log_{a}\displaystyle\frac{1}{N}=-\log_{a}N\)
(3)
\(M=a^p\) の両辺を\(r\)乗して
\(M^r=a^{pr}\) (r乗すると指数はr倍)
よって対数の定義から
\(\log_{a}M^r=pr\)
\(=r\log_{a}M\)
また、\(\sqrt[r]{M}=M^{\frac{1}{r}}\) から
\(\log_{a}\sqrt[r]{M}=\log_{a}M^{\frac{1}{r}}=\displaystyle\frac{1}{r}\log_{a}M\)
が得られる。
ただ、この公式を使いこなすには慣れが必要だと思います。色々演習を積み重ねましょう。
※ここまでは、すべて底\(a\) が共通した公式になっていますが、底がそろっておらずバラバラになっていることももちろんあります。そこで必要になってくるのが次の「底の変換公式」です。
・底の変換公式
\(a,b,c\)を\(1\)ではない正の数とするとき、
底\(a\)の対数、\(\log_{a}b\) を 「底\(c\)に」次のように変換することできます。
\(a,b,c\)を\(1\)でない正の数とするとき
\(\log_{a}b=\displaystyle\frac{\log_{c}b}{\log_{c}a}\)
とくに \(c=b\) とすれば
\(\log_{a}b=\displaystyle\frac{1}{\log_{b}a}\) (底と真数を入れ替えると逆数になる)
(証明)
\(\log_{a}b=p\) とおく。
\(a^p=b\) であり、両辺 底\(c\) の対数をとると・・・(注)
\(\log_{c}a^p=\log_{c}b\)
よって
\(p\log_{c}a=\log_{c}b\) だから、両辺 \(\log_{c}a\) (\(a≠1\) なので0でない) で割ると
\(p=\displaystyle\frac{\log_{c}b}{\log_{c}a}\)
したがって
\(\log_{a}b=\displaystyle\frac{\log_{c}b}{\log_{c}a}\)
(注)
\(M=N\) のとき
指数関数 \(y=c^x\) が 「\(y\)1つに対して\(x\)が1つ対応」していることから
\(M=N=(c^x)\) のとき
\(\log_{c}M=\log_{c}N(=x)\) (これが\(c\)を底とする対数をとるということです)
次回以降これらの公式を利用した計算演習を扱っていきます。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→対数の計算① back→指数方程式と有理数解