対数関数を含む領域図示問題について見ていきます。
(例題)
\(x,y\) は \(x≠1\), \(y≠1\) を満たす正の数で、不等式
\(\log_{x}y+\log_{y}x>2+(\log_{x}2)(\log_{y}2)\)
を満たすとする。このとき\(x,y\) の組 \((x,y)\) の範囲を座標平面上に図示せよ。
(解答)
\(\log_{x}y+\log_{y}x>2+(\log_{x}2)(\log_{y}2)\) より
\(\displaystyle\frac{\log_{2}y}{\log_{2}x}+\displaystyle\frac{\log_{2}x}{\log_{2}y}\)\(>2+(\displaystyle\frac{1}{\log_{2}x})(\displaystyle\frac{1}{\log_{2}y})\)
(一旦 \(\log_{2}x=X\) \(\log_{2}y=Y\) とおいて)
\(\displaystyle\frac{Y}{X}+\displaystyle\frac{X}{Y}\)\(>2+\displaystyle\frac{1}{X}\cdot\displaystyle\frac{1}{Y}\)
通分して整理すると
\(\displaystyle\frac{X^2+Y^2-2XY-1}{XY}>0\)
\(\displaystyle\frac{(X-Y)^2-1}{XY}>0\)
\(\displaystyle\frac{(X-Y+1)(X-Y-1)}{XY}>0\)
何故なら、\(XY\)は負の値もとるので不等号が入れ替わる場合があるからです。
そこで場合分けが必要になってくるので、ひとまずもとの\(\log\)の式にして検討していきます。
\(\displaystyle\frac{(\log_{2}\displaystyle\frac{x}{y}+1)(\log_{2}\displaystyle\frac{x}{y}-1)}{\log_{2}x\log_{2}y}>0\)・・・①
(1)①の (分母)>0 になるとき、つまり「\(x>1\) かつ \(y>1\)」 または 「\(0<x<1\) かつ \(0<y<1\)」のとき
(分子)>0 だから
\(\log_{2}\displaystyle\frac{x}{y}<-1\) または \(\log_{2}\displaystyle\frac{x}{y}>1\)
\(\log_{2}\displaystyle\frac{x}{y}<\log_{2}\displaystyle\frac{1}{2}\) または \(\log_{2}\displaystyle\frac{x}{y}>\log_{2}2\)
よって
\(\displaystyle\frac{x}{y}<\displaystyle\frac{1}{2}\) または \(\displaystyle\frac{x}{y}>2\)
\(y>0\) だから \(y\)倍して整理すると
\(y>2x\) または \(y<\displaystyle\frac{1}{2}x\)
「\(x>1\) かつ \(y>1\)」 または 「\(0<x<1\) かつ \(0<y<1\)」のとき
\(y>2x\) または \(y<\displaystyle\frac{1}{2}x\) です。
「または」はどちらか一方を満たしていればよいので、
(ア)「\(x>1\) かつ \(y>1\)」のとき \(y>2x\) または \(y<\displaystyle\frac{1}{2}x\)
(イ)「\(0<x<1\) かつ \(0<y<1\)」のとき \(y>2x\) または \(y<\displaystyle\frac{1}{2}x\)
と分けて考えることができます。結局これらを図示すると全部で4つの領域になります。
(2)①の (分母)<0 になるとき、つまり「\(x>1\) かつ \(0<y<1\)」 または 「\(0<x<1\) かつ \(y>1\)」のとき
①の (分子)<0 だから
\(-1<\log_{2}\displaystyle\frac{x}{y}<1\)
\(\displaystyle\frac{1}{2}<\displaystyle\frac{x}{y}<2\)
整理して
\(\displaystyle\frac{1}{2}x<y<2x\)
以上(1)(2)より \((x,y)\) の範囲を図示すると次の通り。
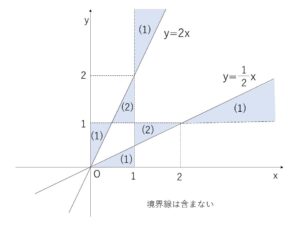
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→対数と無理数 back→対数方程式の解の個数