3つの集合の要素の個数 | 教えて数学理科

3つの集合の和集合の要素の数え方について考えていきます。

・3つの集合の和集合の要素の個数
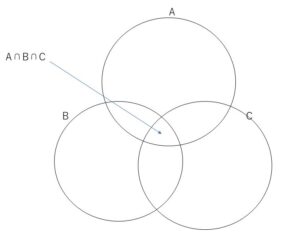
3つの集合\(A,B,C\)について、その和集合の要素の個数\(n(A \cup B \cup C)\)は次のように表されます。

\(n(A \cup B \cup C)\)
\(=n(A)+n(B)+n(C)\)\(-n(A \cap B)-n(B \cap C)-n(C \cap A)\)\(+n(A \cap B \cap C)\)

3集合　要素の個数

2集合の要素の個数と同じように、まずそれぞれを足して、\(A,B\)、\(B,C\)、\(C,A\)の共通部分を引きます。ただこのままだと\(A,B,C\)の3重に重なったものを3個引いたことになるので、\(A,B,C\)の共通部分を数え上げて無いことになります。よって調整のために最後に\(A,B,C\)の共通部分の個数を1つだけ足してあげます。

※なお共通部分が無い場合は、上の式の共通部分の要素の個数を0として考えればよいです。

(例題)
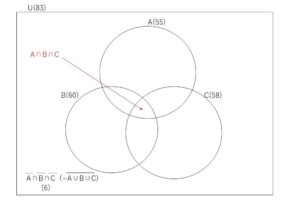
集団検診で \(A,B,C\)の3種の検査を行った。総員数83人中、\(A\)検査に55人、\(B\)検査に60人、\(C\)検査に58人が合格したが、これらの中、\(C,A\)両検査に42人、\(A,B\)両検査に41人、\(B,C\)両検査に45人がそれぞれ合格した。3種の検査にいずれにも合格しなかった人は6人だった。3種の検査すべてに合格した人は何人か。

ベン図もあわせて考えます。

(解答)
\(A,B,C\)の検査に合格した人の集合を\(A,B,C\)とし、全体集合を\(U\)とする。
\(n(U)=83\),　\(n(A)=55\),　\(n(B)=60\),　\(n(C)=58\)
\(n(C \cap A)=42\),　\(n(A \cap B)=41\),　\(n(B \cap C)=45\)
\(n(\overline A \cap \overline B \cap \overline C)=6\)

3集合　要素個数　例題

よって
\(n(A \cup B \cup C)=n(U)-n(\overline A \cap \overline B \cap \overline C)\)\(=83-6=77\)

したがって、
\(n(A \cup B \cup C)\)
\(=n(A)+n(B)+n(C)\)\(-n(A \cap B)-n(B \cap C)-n(C \cap A)\)\(+n(A \cap B \cap C)\)　より

\(77=55+60+58-41-45-42+n(A \cap B \cap C)\)
ゆえに、\(n(A \cap B \cap C)=\)\(32(人)\)

3つの集合により、ベン図ではいろいろな領域ができますが、どの領域の集合の要素の個数が聞かれているかは問題の都度違うので、その都度ベン図で考えてください。

以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。

→高校数学TOP　next→倍数の個数　 back→2つの集合の要素の個数