等比数列の一般項

等比数列の基礎です。

・等比数列
数列

\(2,6,18,54,162,486,\cdots\)

は、初項\(2\)に\(3\)を次々と掛けることによって得られ、ある項とその1つ前の項の比の値が常に\(3\)で一定です。

一般に数列
\(a_1,a_2,\cdots,a_n,a_{n+1},\cdots\)
において、各項に一定の数\(r\)を掛けると次の項が得られるとき、この数列を等比数列といい、比の値\(r\)を公比とよびます。このとき、隣り合う項\(a_n,a_{n+1}\)には次のような関係があります。

\(a_{n+1}=ra_{n}\)・・・①　(前の項に\(r\)を掛けると次の項が得られる)

ここで、初項\(a_1\)と公比\(r\)がどちらも\(0\)でないときは、どの項も\(0\)にはらないので①より

\(\displaystyle\frac{a_{n+1}}{a_n}=r\)　(隣の項との比は\(r\)で一定)

となります。

次に、等比数列の一般項がどうなるかを考えます。
数列\(\{a_n\}\)が初項\(a\)、公比\(r\)の等比数列であるとき

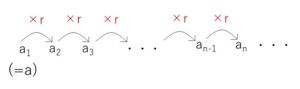
\(a_1=a\)
\(a_2=ar=ar^{2-1}\)
\(a_3=ar×r=ar^2=ar^{3-1}\)
\(a_4=ar^2×r=ar^3=ar^{4-1}\)
\(\cdots\)

\(a_n\)は初項\(a\)に公比\(r\)を\((n-1)\)回掛けたものになるので、一般項\(a_n\)はつぎのようになります。

\(a_n=ar^{n-1}\)　(等比数列の一般項)

(例題1)
\(□,-6,2,□,\cdots\) は等比数列である。\(□\)に入る数字を求めよ。また一般項も求めよ。

(解答)
\(a_1,-6,2,a_4\) とすると、公比\(r\)は

\(r=\displaystyle\frac{2}{-6}\)\(=-\displaystyle\frac{1}{3}\)

よって
\(-6=-\displaystyle\frac{1}{3}a_1\) より
\(a_1=18\)

また
\(a_4=-\displaystyle\frac{1}{3}\cdot2\)
\(a_4=-\displaystyle\frac{2}{3}\)

したがって一般項は、初項\(18\)、公比\(-\displaystyle\frac{1}{3}\)より
\(a_n=18×(-\displaystyle\frac{1}{3})^{n-1}\)

(例題2)
等比数列\(\{a_n\}\)において、\(a_2=2-\sqrt{2}\), \(a_4=10-7\sqrt{2}\) である。この数列\(\{a_n\}\)の一般項を求めよ。

(解答)
\(a_n=ar^{n-1}\) とおくと

\(ar=2-\sqrt{2}\)・・・①
\(ar^3=10-7\sqrt{2}\)・・・②

②より
\(ar\cdot r^2=10-7\sqrt{2}\)
①を代入して
\(r^2(2-\sqrt{2})=10-7\sqrt{2}\)

\(r^2=\displaystyle\frac{10-7\sqrt{2}}{2-\sqrt{2}}\)

\(=3-2\sqrt{2}\) (\(>0\))

よって
\(r=±\sqrt{3-2\sqrt{2}}\)
\(=±\sqrt{(\sqrt{2}-1)^2}\)
\(=±(\sqrt{2}-1)\)

①より
\(a=\displaystyle\frac{2-\sqrt{2}}{r}\)

\(=\displaystyle\frac{2-\sqrt{2}}{±(\sqrt{2}-1)}\)

\(=\displaystyle\frac{\sqrt{2}(\sqrt{2}-1)}{±(\sqrt{2}-1)}\)

\(=±\sqrt{2}\)

したがって一般項は
\(a_n=\sqrt{2}(\sqrt{2}-1)^{n-1}\)
または
\(a_n=-\sqrt{2}(1-\sqrt{2})^{n-1}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→等比数列をなす3数　back→方程式の解と等差数列