群数列の例題です。
(例題1)
自然数\(p,q\)の組 \((p,q)\) を
(A)\(p+q\) の値の小さい組から大きい組へ
(B)\(p+q\) の値の同じ組では、\(p\)の値が大きい組から小さい組へ
という規則に従って、次のように1列に並べる。
\((1,1),(2,1),(1,2),(3,1),(2,2),(1,3),\cdots\)
(1)組\((m,n)\)は、初めから何番目にあるか。
(2)初めから\(100\)番目にある組を求めよ。

和\(p+q\)が同じであるものを群として分けます。すると
(i)\(k\)群では \(p+q-1=k\) (1つずれていることに注意)
(ii)\(k\)群の項数は\(k\)項
という規則になっています。(B)は左側の数字\(p\)が大きい順に並んでいるということですが、逆にいうと右側の数字\(q\)が小さい順に並んでいるということです。
(解答)
(1)

組\((m,n)\)は、第\(m+n-1\)群の第\(n\)項。
\(k\)群には\(k\)個の項があるから、(第\(m+n-2\)群までの項数)\(+n\)を考えて
\(\{1+2+\cdots+(m+n-2)\}+n\)
\(=\displaystyle\frac{1}{2}(m+n-2)(m+n-1)+n\)
したがって
\(\displaystyle\frac{1}{2}(m+n-2)(m+n-1)+n\) 番目
(2)
初めから\(100\)番目が第\(k\)群にあるとすると、第\(i\)群には\(i\)個の項があるから
\(1+2+\cdots+(k-1)<100≦1+2+\cdots+k\)
\(\displaystyle\frac{1}{2}(k-1)k<100≦\displaystyle\frac{1}{2}k(k+1)\)
この不等式を満たす自然数\(k\)は \(k=14\) だから、第\(14\)群にある。
最初から第\(13\)群までの最後までの項数は
\(\displaystyle\frac{1}{2}\cdot13\cdot14=91\)
だから、\(100\)番目は第\(14\)群の第\(9\)項。
よって組\((p,q)\) において、\(q=9\) であり、\(p+q-1=14\) より
\(p=6\)
したがって\(100\)番目は
\((6,9)\)
(例題2)
図のように並んだ数がある。いま、そこから数字を
\((1),(2,3),(4,6,5),(8,12,10,7),(16,24,20,14,9),\cdots\)
のように斜めにとり出し、これらを順に第\(1\)群、第\(2\)群、第\(3\)群、・・・と呼ぶことにする。
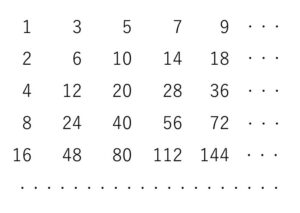
(1)第\(n\)群の中の第\(k\)項を求めよ。
(2)第\(n\)群中にある\(n\)個の数の和を求めよ。
群数列自体の規則性が見つけにくいので、全体の数字の並びの法則を探します。
すると縦方向が等比数列、横方向が等差数列になっていることに気づきます。
これらのことを利用するのですが、解答では縦方向の等比数列に着目していきます。
(解答)
(1)

縦方向の等比数列に着目すると、第\(n\)群の初項は\(2^{n-1}\)です。第2項は図で右斜め上(上に1つ、右に1つ移動)なので、指数は1つ減り、係数は1→3 と2つ増えます。第3項は指数がさらに1つ減り、係数は3→5 と2つ増え・・・と繰り返しです。
第\(n\)群の初項は\(2^{n-1}\)。第\(n\)群において項が1つ増えると\(2\)の指数は1つ減り、係数は2つ増えるので、項を並べて書くと
\(2^{n-1},\ 3\cdot2^{n-2},\ 5\cdot2^{n-3},\ 7\cdot2^{n-4},\cdots\)
したがって第\(n\)群の第\(k\)項は
\((2k-1)2^{n-k}\)
(2)
求める和を\(S\)とすれば(1)より
\(\hspace{5pt}S=1\cdot2^{n-1}+3\cdot2^{n-2}+5\cdot2^{n-3}+\cdots+(2n-1)2^{0}\)
\(\displaystyle\frac{S}{2}=\hspace{45pt}1\cdot2^{n-2}+3\cdot2^{n-3}+\cdots+(2n-3)2^{0}+(2n-1)2^{-1}\)
\(S-\displaystyle\frac{S}{2}\) より
\(\displaystyle\frac{S}{2}=2^{n-1}+2\cdot2^{n-2}+2\cdot2^{n-3}+\cdots+2\cdot2^{0}-(2n-1)\cdot\displaystyle\frac{1}{2}\)
両辺\(2\)倍して
\(S=2^{n}+4(2^{n-2}+2^{n-3}+\cdots+2^{0})-(2n-1)\)
(括弧内は反対から見て 初項\(1\)、公比\(2\)、項数\(n-1\) の等比数列の和だから)
\(=2^{n}+4\cdot\displaystyle\frac{2^{n-1}-1}{2-1}-2n+1\)
\(=2^{n}+4\cdot2^{n-1}-4-2n+1\)
(\(4\cdot2^{n-1}=2\cdot2^{n}\) より)
\(=3\cdot2^{n}-2n-3\)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→格子点の数 back→群数列①