確率変数の期待値

確率変数の期待値について見ていきます。
確率変数を用いない通常の期待値と内容は同じです。

・確率変数の期待値

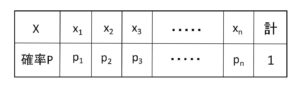
確率変数がおおよそどの値になるか(どの程度の値が期待されるか)を表すのに、期待値が利用されます。各\(X\)の値に対応する確率は全体に占める割合になっているので、期待値\(E(X)\)は各\(X\)の値と確率の積を考えて次のように定義されます。

\(E(X)=\displaystyle\sum_{k=1}^{n}x_kp_k\)
\(=x_1p_1+x_2p_2+x_3p_3+\cdots+x_np_n\)

\(E(X)\)の\(E\)は Expectation (期待値) の頭文字です。期待値を表すのに単に文字\(m\)や\(μ\)を用いることもあります。
また、期待値はだいたい全体の\(X\)の真ん中あたりの値になるので、平均値とよばれることもあります。

(例題)
点\(P\)が数直線上を原点から出発して動く。硬貨を投げて表が出れば\(P\)は正の方向に\(2\)だけ動き、裏が出れば負の方向に\(1\)だけ動く。\(4\)回硬貨を投げたときの点\(P\)の座標を確率変数\(X\)とする。\(X\)の確率分布を求めて、\(X\)の期待値を求めよ。

(解答)
表が出る回数を\(k\)回 (\(0≦k≦4\)) とすると、裏が出る回数は\(4-k\)回。
表が\(k\)回出る確率\(p_k\)は
\(p_k={}_4\mathrm{C}_{k}(\displaystyle\frac{1}{2})^{k}(\displaystyle\frac{1}{2})^{4-k}={}_4\mathrm{C}_{k}(\displaystyle\frac{1}{2})^{4}\)・・・①

表\(k\)回に対応する\(P\)の座標\(X\)は
\(X=2k-(4-k)=3k-4\)・・・②

①②で \(k=0,1,2,3,4\) を代入することで確率分布は次のように得られる。

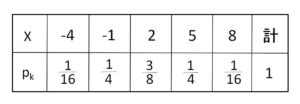
したがって期待値は
\(E(X)=(-4)\cdot\displaystyle\frac{1}{16}+(-1)\cdot\displaystyle\frac{1}{4}+2\cdot\displaystyle\frac{3}{8}+5\cdot\displaystyle\frac{1}{4}+8\cdot\displaystyle\frac{1}{16}\)

\(=2\)

(\(X=2\)を中心に対称に分布していることからも分かる)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→確率分布と分散・標準偏差　back→確率変数と確率分布