確率変数の変換(1次式)

1次式により確率変数を変換すると、期待値や分散がどうなるか見ていきます。
結果は数IAのデータの分析の場合と同じです。

・確率変数の変換(1次式)
確率変数\(X\)が、\(x_1,x_2,\cdots,x_n\)という値をとるとき、変数\(Y\)が \(Y=aX+b\) を満たすとき、\(Y\)も \(ax_1+b,ax_2+b,\cdots,ax_n+b\) という値をとる確率変数になります。
このような\(Y\)を考えることを確率変数の変換とよびます。
\(X\)が\(x_k\)という値をとる確率と、\(Y\)が\(ax_k+b\)という値をとる確率は同じなので、\(Y\)の確率分布は次のようになります。

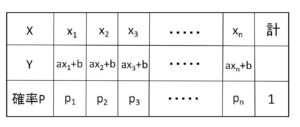
1次式による変換 \(Y=aX+b\) (\(a,b\)は定数) において、\(Y\)の期待値・分散・標準偏差は、それぞれの定義から\(X\)の期待値・分散・標準偏差を用いて次のように表されることが分かります。

証明の前にこれらの等式が成り立つ意味について考えてみます。

まず期待値については、\(X\)を\(a\)倍して\(b\)足していることから、分布も全体として\(a\)倍拡大縮小され、\(+b\)だけ平行移動されることになるので、期待値も同様の動きをします。
一方、分散や標準偏差は\(a\)倍されることにより散らばりもその分だけ広がる(縮まる)ことになりますが、\(+b\)だけ平行移動しても全体が同じだけ動くため散らばりは変化しないので、\(b\)は影響がないことになります(等式にも現れない)。分散で\(a\)が2乗されているのは、分散が2乗和であることが由来です。

(証明)
期待値について
\(E(Y)=E(aX+b)\)
\(=(ax_1+b)p_1+(ax_2+b)p_2+\cdots+(ax_n+b)p_n\)
\(=a(x_1p_1+x_2p_2+\cdots+x_np_n)+b(p_1+p_2+\cdots+p_n)\)
\(=aE(X)+b\)

分散について
\(E(X)=m\) とおくと、\(E(Y)=am+b\) だから

\(V(Y)=V(aX+b)\)
\(=\{ax_1+b-(am+b)\}^2p_1+\{ax_2+b-(am+b)\}^2p_2+\cdots+\{ax_n+b-(am+b)\}^2p_n\)
\(=a^2\{(x_1-m)^2p_1+(x_2-m)^2p_2+\cdots+(x_n-m)^2p_n\}\)
\(=a^2V(X)\)

標準偏差について
\(σ(Y)=\sqrt{V(Y)}=\sqrt{a^2V(X)}\)
\(=|a|\sqrt{V(X)}\)
\(=|a|σ(X)\)

(例題)
点\(P\)が数直線上を原点から出発して動く。硬貨を投げて表が出れば\(P\)は正の方向に\(2\)だけ動き、裏が出れば負の方向に\(1\)だけ動く。\(4\)回硬貨を投げたときの点\(P\)の座標を確率変数\(Y\)とする。

(1)表が出る回数を確率変数\(X\)とするとき、\(X\)の期待値・分散・標準偏差を求めよ。
(2) (1)を利用して\(Y\)の期待値・分散・標準偏差を求めよ。

(解答)
(1)
\(k\)回表が出るとき (\(k=0,1,2,3,4\))、その確率\(p_k\)は
\(p_k={}_4\mathrm{C}_k(\displaystyle\frac{1}{2})^{k}(\displaystyle\frac{1}{2})^{4-k}={}_4\mathrm{C}_k(\displaystyle\frac{1}{2})^4\)

よって\(X\)の確率分布は次のようになる。

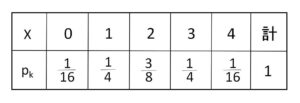
したがって\(X\)の期待値は
\(E(X)=1\cdot\displaystyle\frac{1}{4}+2\cdot\displaystyle\frac{3}{8}+3\cdot\displaystyle\frac{1}{4}+4\cdot\displaystyle\frac{1}{16}\)

\(=2\)

分散は
\(V(X)=E(X^2)-\{E(X)\}^2\)
\(=1\cdot\displaystyle\frac{1}{4}+2^2\cdot\displaystyle\frac{3}{8}+3^2\cdot\displaystyle\frac{1}{4}+4^2\cdot\displaystyle\frac{1}{16}-2^2\)

\(=1\)

標準偏差は
\(σ(X)=\sqrt{1}=1\)

(2)

裏が出る回数は \(4-X\) 回なので座標\(Y\)は
\(Y=2X-(4-X)=3X-4\)

よって\(Y\)の期待値・分散・標準偏差はそれぞれ
\(E(Y)=E(3X-4)\)
\(=3E(X)-4\)
\(=3\cdot2-4\)
\(=2\)

\(V(Y)=V(3X-4)\)
\(=3^2V(X)\)
\(=9\cdot1\)
\(=9\)

\(σ(Y)=σ(3X-4)\)
\(=|3|σ(X)\)
\(=3\cdot1\)
\(=3\)

(\(V(Y)=9\) より \(σ(Y)=\sqrt{9}=3\) と求めてもよいです)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→確率変数の独立　back→確率変数の分散・標準偏差