母比率と標本比率

母比率と標本比率の性質について見ていきます。

 

・母比率と標本比率

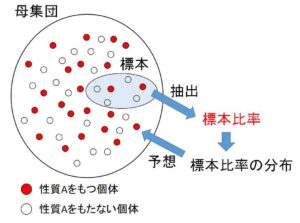
母集団の特徴を決める量として母平均の他に、ある特定の性質をもつ個体の割合を考えることもあります。ある政党の支持率 や ある工場の製品の不良品の割合 などがその例です。

一般に、母集団のなかである性質\(A\)をもつ個体の割合\(p\)を、この性質をもつ個体の母集団における母比率といいます。\(p\)は\(0\)から\(1\)の間の数です。

また、調査のためにこの母集団からいくらか標本を抽出するとき、この標本のうち性質\(A\)をもつ個体の割合を、この性質に対する標本比率とよびます。標本比率は確率変数として表すとき通常、文字 \(R\ (r)\) を用います。
標本比率は平均でいう標本平均に対応し、標本の抽出数を増やして(標本の大きさ\(n\)を大きくして)標本比率の分布を考えたり、標本比率から母比率を予想(推定)したります。

母集団はある性質\(A\)を 「もつ か もたない」 (それぞれ \(p,1-p\) の割合) で分類できるので、母比率は二項分布と深い関わりを持っています。

 

 

・標本比率の分布
標本比率の期待値・分散・標準偏差は次のようになり、また\(n\)を十分大きくすると近似的に正規分布に従います。(復元抽出とみなすことにする。また母比率は\(p\)とする。)

(解説)
導出では、二項分布を利用する方法と標本平均を利用する方法を紹介します。
標本平均を利用する方法のほうが、標本平均との対応が分かりやすいと思います。

(二項分布を利用する方法)
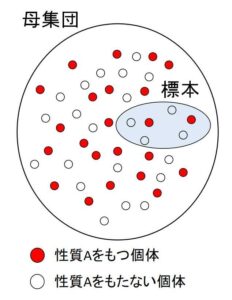
標本のうち性質\(A\)をもつ個体の個数を\(W\)とする。復元抽出とみなせるとき、\(W\)は標本のうち特性をもつ個体の総数なので、二項分布 \(B(n,p)\) に従うことになる。
標本比率は\(R\)は\(W\)を用いて
\(R=\displaystyle\frac{W}{n}\)
と表せる。(上図でいうと\(W\)は標本のうちの赤丸の個数、\(R\)は標本のうち赤丸の割合になる)

\(W\)の期待値と分散は二項分布に従うことから
\(E(W)=np\)、\(V(X)=np(1-p)\)

よって
\(E(R)=E(\displaystyle\frac{W}{n})=\displaystyle\frac{1}{n}E(W)\)

\(=\displaystyle\frac{1}{n}\cdot np\)

\(=p\)

\(V(R)=V(\displaystyle\frac{W}{n})=\displaystyle\frac{1}{n^2}V(W)\)

\(=\displaystyle\frac{1}{n^2}\cdot np(1-p)\)

\(=\displaystyle\frac{p(1-p)}{n}\)

ゆえに
\(σ(R)=\sqrt{\displaystyle\frac{p(1-p)}{n}}\)

また、\(n\)が十分大きいとき\(W\)は正規分布に近似的に従うので、\(\displaystyle\frac{1}{n}\)倍縮小されただけの\(R\)も近似的に正規分布に従う。

※もう少し簡易的にやると
\(n\)が十分大きいとき、\(W\)を標準化した
\(Z=\displaystyle\frac{W-np}{\sqrt{np(1-p)}}\)
は標準正規分布に従う。\(Z\)を変形すると(分母分子\(n\)で割ると)

\(Z=\displaystyle\frac{\displaystyle\frac{W}{n}-p}{\sqrt{\displaystyle\frac{p(1-p)}{n}}}=\)\(\displaystyle\frac{R-p}{\sqrt{\displaystyle\frac{p(1-p)}{n}}}\)

となることから、\(R\)が近似的に期待値\(p\)、標準偏差\(\sqrt{\displaystyle\frac{p(1-p)}{n}}\)の正規分布に従うことが分かる。

 

(標本平均を利用する方法)
母集団において、「性質\(A\)をもつ個体は変量\(1\)、もたない個体は変量\(0\)」で表すことにして、これらの変量をとる確率変数を\(X\)とする。
\(n\)個標本を抽出(復元抽出)するとき、各個体の変量に対応する確率変数を \(X_1,X_2,\cdots,X_n\) とおくと、これら各変数は\(X\)と同じ分布をとる。

すると標本平均
\(\overline{X}=\displaystyle\frac{X_1+X_2+\cdots+X_n}{n}\)
は、標本比率\(R\)と全く同じになるので
\(R=\displaystyle\frac{X_1+X_2+\cdots+X_n}{n}\)

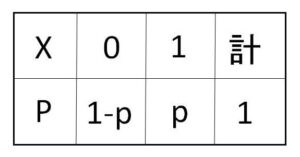
よって母集団分布が上記\(X\)の分布になることから、この母平均・母分散は
\(E(X)=p\)
\(V(X)=0^2\cdot(1-p)+1^2\cdot p-p^2\)
\(=p(1-p)\)

したがって\(R\)の期待値・分散・標準偏差は、標本平均のこれらと同様に
\(E(R)=p\)、\(V(R)=\displaystyle\frac{p(1-p)}{n}\)、\(σ(R)=\sqrt{\displaystyle\frac{p(1-p)}{n}}\)

また\(n\)を十分大きくすると、中心極限定理より\(R\)は近似的に正規分布に従う。

 

 

 

(例題)
\(A\)地区で収穫されるジャガイモには、1個の重さが\(200\mathrm{g}\)を超えるものが\(25％\)含まれることが経験的に分かっている。\(A\)地区で収穫されたジャガイモから\(400\)個を無作為に抽出し、重さを計測した。この\(400\)個のジャガイモのうち\(200\mathrm{g}\)を超えるものの個数を確率変数\(W\)とする。また、\(200\mathrm{g}\)を超えるジャガイモの標本における比率を、\(R=\displaystyle\frac{W}{400}\) とする。\(A\)地区で収穫されるジャガイモ全体のうち\(200\mathrm{g}\)を超えるものの割合を\(25％\)とすることにして、以下の問いに答えよ。

(1)\(R\)の期待値と標準偏差を求めよ。
(2)標本の大きさ\(400\)は十分大きいので、\(R\)は近似的に正規分布に従う。この正規分布の期待値と分散を求めよ。
(3)\(P(R≧x)=0.0465\) となる\(x\)の値を求めよ。ただし \(\sqrt{3}=1.73\) とし、小数第3位まで求めよ。なお\(Z\)が標準正規分布に従うとき \(P(0≦Z≦1.68)=0.4535\) である。

 

(解答)
(1)

(解答1)
\(W\)は二項分布 \(B(400,0.25)\) に従うので
\(E(W)=400\cdot0.25=100\)
\(σ(W)=\sqrt{400\cdot0.25\cdot0.75}=\sqrt{75}\)

よって \(R=\displaystyle\frac{W}{400}\) より
\(E(R)=E(\displaystyle\frac{W}{400})=\displaystyle\frac{1}{400}E(W)\)
\(=\displaystyle\frac{1}{400}\cdot100\)
\(=\displaystyle\frac{1}{4}\)　(\(25％\))

\(σ(R)=σ(\displaystyle\frac{W}{400})=\displaystyle\frac{1}{400}σ(W)\)
\(=\displaystyle\frac{\sqrt{75}}{400}\)
\(=\displaystyle\frac{\sqrt{3}}{80}\)

(解答2)
母比率は \(p=0.25\)、標本の大きさは \(n=400\) だから
\(E(R)=0.25=\displaystyle\frac{1}{4}\)

\(σ(R)=\sqrt{\displaystyle\frac{0.25\cdot0.75}{400}}=\displaystyle\frac{\sqrt{3}}{80}\)

(2)
(1)より\(R\)の期待値と分散はそれぞれ
\(\displaystyle\frac{1}{4}\)、\(\displaystyle\frac{3}{6400}\)

(3)
\(Z=\displaystyle\frac{R-\displaystyle\frac{1}{4}}{\displaystyle\frac{\sqrt{3}}{80}}\)

は標準正規分布に従う。
\(P(0≦Z≦1.68)=0.4535\) より
\(P(Z≧1.68)=0.5-0.4535=0.0465\)

よって
\(P(\displaystyle\frac{R-\displaystyle\frac{1}{4}}{\displaystyle\frac{\sqrt{3}}{80}}≧1.68)=0.0465\)

中身の不等式を整理すると
\(\displaystyle\frac{R-\displaystyle\frac{1}{4}}{\displaystyle\frac{\sqrt{3}}{80}}≧1.68\)

\(R≧1.68\cdot\displaystyle\frac{\sqrt{3}}{80}+\displaystyle\frac{1}{4}=0.28633\)

したがって
\(x=0.286\)

 

 

 

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→母比率と二項分布　back→中心極限定理・大数の法則