領域を利用した命題に関する問題について見ていきます。
(例題1)
\(x,y\)は実数とする。\(|x|+|y|≦1\)・・・① ならば \(|x+y|≦1\)・・・② であることを証明せよ。
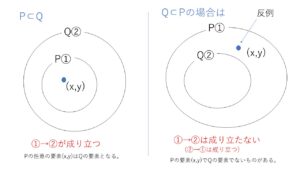
①ならば②が成り立つことを示したいので、①の表す領域が②の表す領域に含まれていることを示せばよいことになります。つまり ①の満たす領域を\(P\),②の満たす領域を\(Q\)とすれば、\(P \subset Q\) を示すことになります。
(①を満たす全ての\((x,y)\)について、②を満たすを示すことになるので、①のほうが内側になればよい)
(解答)
②は \(-1≦x+y≦1\)
よって、①の表す領域\(P\),②の表す領域\(Q\)を図示すると次の通り。
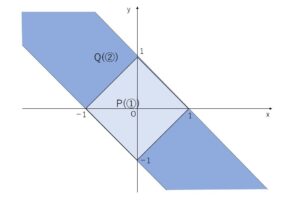
\(P \subset Q\) となるので、①ならば②が成り立つ。
(②は①であるための必要条件となる)
(例題2)
\(x^2+y^2-2x\)\(+2y<6\) を満たすすべての実数\(x,y\)が、\(x^2+y^2\)\(>a-8x+2y\) を満たすような\(a\)の値の範囲を求めよ。
\(x^2+y^2-2x\)\(+2y<6\)・・・① の表す領域を\(P\),
\(x^2+y^2\)\(>a-8x+2y\)・・・② の表す領域を\(Q\)とすれば、\(P \subset Q\) が成り立つ\(a\)の値の範囲を求めることになります。
①②は円の方程式になりそうなので、平方完成してみます。
(解答)
\(x^2+y^2-2x\)\(+2y<6\)・・・① の表す領域を\(P\),
\(x^2+y^2\)\(>a-8x+2y\)・・・② の表す領域を\(Q\)とする。
①は \((x-1)^2+(y+1)^2\)\(<8\)・・・①’
②は \((x+4)^2+(y-1)^2\)\(>a+17\)・・・②’
②’について。まず \(a<-17\) のときは②’は円の方程式にはなりませんが、\(a<-17\) のとき ②’の左辺は\(0\)以上、右辺は負なので②’を満たす\(x,y\)はすべての実数となります。よって\(Q\)は\(xy\)平面全体なので、\(P \subset Q\)が成り立ちます。
他の\(a=-17\), \(a>-17\) のときも同様に考えていきます。
(ア)\(a<-17\) のとき
②’の左辺は\(0\)以上、右辺は負なので②’を満たす\(x,y\)はすべての実数である。
よって、\(P \subset Q\)が成り立ち条件を満たす。
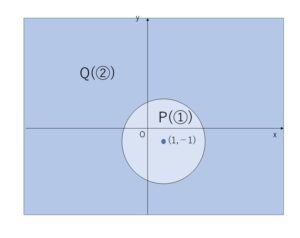
(イ)\(a=-17\) のとき
②’は \((x+4)^2+(y-1)^2\)\(>0\) 。よって \((x,y)=(-4,1)\) 以外の全ての\(x,y\)について②’は成り立つ。
①’に\((x,y)=(-4,1)\) を代入すると、\(25+4\)\(<8\) なので、\((x,y)=(-4,1)\) は①’に含まれない。よって、\(P \subset Q\)が成り立ち条件を満たす。
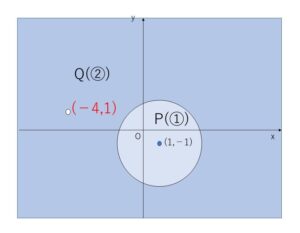
(ウ)\(a>-17\) のとき
外接しているときも、接点は\(P,Q\)どちらにも含まれないので、接点以外について考えると \(P \subset Q\)が成り立つことがわかります。
(外側にある場合)
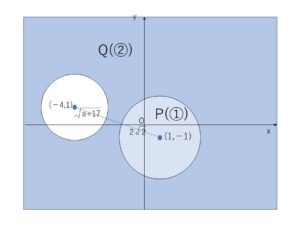
(外接している場合)
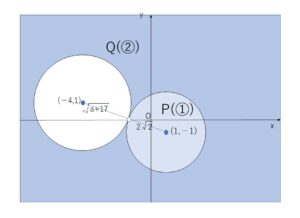
\((x-1)^2+(y+1)^2\)\(<(2\sqrt{2})^2\)・・・①’ (領域\(P\))
\((x+4)^2+(y-1)^2\)\(>(\sqrt{a+17})^2\)・・・②’ (領域\(Q\)) について
\(P \subset Q\) となるためには、①’②’の境界線の円が互いに外側にあるか、外接しなければならない。中心間の距離は \(\sqrt{5^2+2^2}=\sqrt{29}\) だから
\(2\sqrt{2}+\sqrt{a+17}≦\sqrt{29}\)
\(\sqrt{a+17}≦\sqrt{29}-2\sqrt{2}\)
両辺正の値なので2乗して
\(a+17≦37-4\sqrt{58}\)
よって
\(a≦20-4\sqrt{58}\)
\(a>-17\) とあわせて
\(-17<a≦20-4\sqrt{58}\)
以上より
\(a≦20-4\sqrt{58}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→通過領域① back→線形計画法(文章問題)