微分を利用した高次方程式(主に3次方程式)の実数解の個数に関する問題について扱っていきます。
→(3-5)3次関数のグラフの特徴① を参考にしてください。
(例題1)
(1)方程式 \(x^3-3x^2+3=0\) の実数解の個数を求めよ。
(2)曲線 \(y=x^3-2x+1\) と 直線 \(y=x+k\) が異なる3点を共有するような実数の定数\(k\)の値の範囲を求めよ。
(解答)
(1)
\(y=x^3-3x^2+3\) とおく
\(y’=3x(x-2)\) より、増減表とグラフは次の通り。
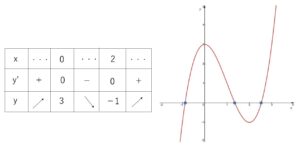
グラフと\(x\)軸との交点は3個あるので、
\(x^3-3x^2+3=0\) の実数解の個数は3個。
「\(f(-1)<0\), \(f(0)>0\)」, 「\(f(1)>0\), \(f(2)<0\), \(f(3)>0\)」 より3つの実数解はそれぞれ
「\(-1<x<0\), \(1<x<2\), \(2<x<3\)」 の範囲にあります。
(2)
\(y=x^3-2x+1\) , \(y=x+k\) より \(y\)を消去して
\(x^3-2x+1=x+k\)
\(x^3-3x+1=k\) (定数分離)
として、今度は \(y=x^3-3x+1\)・・・① と \(y=k\)・・・② の共有点の個数の変化を考えます。
定数分離する意味は、①のグラフに文字定数が無いので固定されたグラフで考えることができて、さらに②のグラフは\(x\)軸に平行(横に真っ直ぐ)だから、\(k\)を変化させても横に真っ直ぐなグラフが上下するだけなので簡単に共有点の個数の変化を追えるからです。
\(x^3-3x+1=k\) として
\(y=x^3-3x+1\)・・・① と \(y=k\)・・・② が異なる3つの共有点をもつ場合を考える。
①のグラフは
\(y’=3(x+1)(x-1)\) より
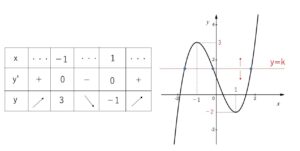
②を動かすと異なる3つの共有点をもつときは
\(-1<k<3\)
(例題2)
方程式
\(\log_{3}x+\log_{\sqrt{3}}(3-x)+\log_{3}\displaystyle\frac{1}{a}=0\)
について
(1) \(a\) を\(x\)の式 (\(f(x)\)とする)で表せ。
(2) \(y=f(x)\) のグラフをかけ。
(3) 与えられた方程式を満たす異なる実数解の個数はいくつあるか。定数\(a\)の値で分類して答えよ。
(解答)
(1)
真数条件から
\(x>0\), \(3-x>0\), \(\displaystyle\frac{1}{a}>0\)
よって
\(0<x<3\), \(a>0\)
\(\log_{3}x+\log_{\sqrt{3}}(3-x)+\log_{3}\displaystyle\frac{1}{a}=0\) より
\(\log_{3}x+\displaystyle\frac{\log_{3}(3-x)}{\log_{3}\sqrt{3}}=\log_{3}a\)
\(\log_{3}x+2\log_{3}(3-x)=\log_{3}a\)
\(\log_{3}x(3-x)^2=\log_{3}a\)
したがって
\(a=x(3-x)^2\) (\(0<x<3\))
(2)
\(f(x)=x(3-x)^2=x^3-6x^2+9x\)
\(f'(x)=3(x-1)(x-3)\)
よって増減表より、グラフは次の通り。
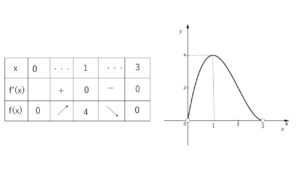
(3)
\(a=x(3-x)^2\) (\(0<x<3\))
の実数解の個数と同じなので、(例題1)(2)と同様に、\(y=a\), \(y=x(3-x)^2\) のグラフの共有点の個数(=実数解の個数)を数えます。
\(y=f(x)\) と \(y=a\) の共有点の個数が、方程式の実数解の個数になるので
\(a>0\) より
\(0<a<4\) のとき 2個
\(a=4\) のとき 1個
\(a>4\) のとき 0個
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→実数解の個数② back→速度・加速度・変化率