4次関数のグラフの特徴

4次関数のグラフの形状の分類について見ていきます。

・4次関数のグラフまとめ
4次関数 \(y=f(x)\) の導関数 \(y=f'(x)\) は3次関数なので、 3次関数の正負の入れ替わり、つまり3次関数と\(x\)軸との交点の個数によって決定されます。 →(3-5)3次関数のグラフの特徴①　でやりましたが、\(x\)軸との交点の個数(3次方程式の解の個数)における分類は次の通りです。(\(y=f(x)\) の4次の係数は正、つまり\(y=f'(x)\) の3次の係数は正とします)

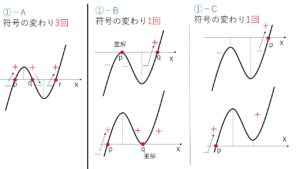
①\(y=f'(x)\) が 極値をもつケース
(\(f^{\prime\prime}(x)=0\) が2つの異なる実数解をもつ)

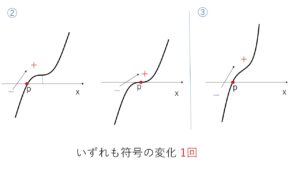
②③\(y=f'(x)\) が 極値をもたないケース
(②は \(f^{\prime\prime}(x)=0\) が重解をもち、③は実数解をもたない)

したがって大きく分けると

(i)符号が3回変化する「①－A」のとき、4次関数 \(y=f(x)\) は極値を3つもち

(ii)符号が1回変化する 「①－B , ①－C , ②, ③」のときは、極値を1つもつ

ことになります。

(ii) についてもう少し細かく分けると
(ア)①－B では、\(f'(x)=0\) となる実数解が2つあるので、接線の傾きが\(0\)となる箇所が2個、
(イ)①－C, ②, ③ では傾きが\(0\)となる箇所が1個(極値のときのみ)

ここまでの分類で4次関数 \(y=f(x)\) について 図示すると次の通りです。

(4次関数のグラフ分類)

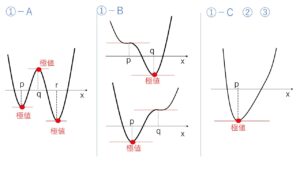
そして、さらに(イ)は変曲点の数で分けることができます。(下記参照)

・変曲点の数
変曲点の数は、2回微分した関数の符号の変化の個数なので

2次方程式　\(f^{\prime\prime}(x)=0\) が

(1)異なる2つの実数解をもつとき、符号の変化は2回なので変曲点は2個
(2)重解をもつとき、実数解をもたないとき、符号の変化はないので変曲点は0個

となります。つまり上の分類だと
「①ーA,B,C 」が変曲点が2個で、「②③」が変曲点0個となります。

・4次関数のグラフの対称性
一般に4次関数のグラフは対称性がありません。

まず点対称性について考えると、
\(y=x^4+ax^3+bx^2+cx+d\) を、
\(x\)軸方向に\(p\),\(y\)軸方向に\(q\)だけ 平行移動すると

\(y=g(x)=(x-p)^4+a(x-p)^3+b(x-p)^2+c(x-p)+d+q\)

となりますが、恒等式
\(g(x)=-g(-x)\)
について考えると、\(x^4\)の項が\(p,q\)の値をどう変化させても残るので原点対称にならず、移動前のグラフは点対称性がありません。

次に線対称性ですが、こちらは認められる場合があります。

平行移動後の方程式が

\(y=x^4+px^2+q\)・・・(1)

の形をしていれば、これが\(y\)軸対称であることから移動前の曲線も\(y\)軸に平行な直線について対称になります。(必ずしも(1)の形にできるとは限りません)

今回は例題はなしです。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→極大値と極小値の和・差 　back→3次関数のグラフの特徴②(対称性)